Bioacoustique
Du signal physique au message sensoriel
Benoît C. FORGET
2018-2019
Département de photonique, Institut de la Vision
UFR des Scicences Fondamentales et Biomédicales
benoit.forget@parisdescartes.fr
Plan
- Ondes acoustiques
- Fluide compressible dans une conduite, Équation de d'Alembert, Solutions harmoniques
- Amplitude, Phase, Énergie. Échelle logarithmique (dB)
- Réflexion et Transmission d'onde : impédance caractéristique et impédance acoustique.
- Oreille capteur de son
- Physiologie de l'oreille
- adaptation d'impédance, rôle de l'oreille moyenne
- Son simple, son complexe, son musical
- Fréquence, représentation spectrale du son
- Notion de résonance, rôle de l'oreille externe
- Oreille interne : analyse spectrale
- Sons voisés : les voyelles
- Intenisité et Sonie (bruyance)
- Modèles physiques simples de psychoacoustique
Ondes acoustiques
Qu'est-ce qu'une onde ?

Dans un milieu élastique il existe des forces internes qui tendent à le ramener à sa situation d'équilibre après une perturbation
Cette perturbation (ou déformation) se déplace à une vitesse (célérité) qui est déterminée uniquement par les propriétés mécaniques de ce milieu.
Une déformation se déplace sans se déformer
Une fonction de deux variables (espace et temps) couplées :
Existe-t-il une équation dont la solution est de la forme :
$$A\xi(x-ct)+B\xi(x+ct)$$
l'équation de d'Alembert !
$$\frac{\partial^2 \xi}{\partial t^2} - c^2 \frac{\partial^2 \xi}{\partial x^2} =0 $$
Analyse dimensionnelle :
$$ \frac{[\xi]}{[T]^2}-[c]^2\frac{[\xi]}{[L]^2} \;\to\; [c]=\frac{[L]}{[T]}$$
La célérité \(c\) a bien les dimensions d'une vitesse.
Newton P.F.D. \(\displaystyle \to\quad \frac{\partial^2 \xi}{\partial t^2}-c^2\frac{\partial^2 \xi}{\partial x^2}=0\)
Si les angles sont petits : \(\displaystyle \sin \theta_{1,2} \approx \tan\theta_{1,2} = \left.\frac{\partial \xi} {\partial z}\right| _{z=z_1,z=z_2}\)
et si la corde ne se déforme pas : \(\displaystyle T_2 \approx T_1 \equiv T_0 \)
et donc : \(\displaystyle F_x(t)= T_0 \left.\frac{\partial \xi}{\partial z}\right|_{z=z_2} -T_0 \left.\frac{\partial \xi}{\partial z}\right|_{z=z_1}= T_0 \Delta z \frac{\partial^2 \xi}{\partial z^2}\)
Il faut d'appliquer la seconde loi de Newton : \(\vec F = m\vec a\).
$$ \xi\to\textrm{déplacement}\; ;\; \frac{\partial \xi}{\partial t}\to\underbrace{\textrm{vitesse}}_{\neq \textrm{célérité !}} \; ;\; \frac{\partial^2 \xi}{\partial t^2}\to \textrm{accélération} $$
La masse linéïque (masse par unité de longueur) \(\rho\) permet d'exprimer la masse \(m\) du segment : \(m=\rho\Delta z\)
$$F_x(t)= ma \to T_0 \Delta z \frac{\partial^2 \xi}{\partial z^2} = \rho \Delta z \frac{\partial^2 \xi}{\partial t^2} \;\to\; \frac{\partial^2 \xi}{\partial z^2} - \frac{\rho}{T_0} \frac{\partial^2 \xi}{\partial t^2} =0$$
P.F.D + élasticité ... \(\displaystyle \to\quad \frac{\partial^2 p}{\partial t^2}-c^2\frac{\partial^2 p}{\partial x^2}=0\)
La déformation \(\xi\) est fonction du temps \(t\) et de la position \(x\), de la forme : \(\xi(x,t) = f(x-ct)\).
$$ F=ma \quad\to\quad S
\underbrace{\left[p(x) - p(x+\Delta x) \right]}_{=-\frac{\partial p}{\partial x} \Delta x}
= \rho S \Delta x \frac{\partial^2\xi}{\partial t^2} $$
\[ -\frac{\partial p}{\partial x} = \rho \frac{\partial^2\xi}{\partial t^2} \quad\to\quad \frac{\partial p}{\partial x} + \rho \frac{\partial^2\xi}{\partial t^2} = 0\]
\[ \rho V = \rho_0 V_0 \;\to\; \frac{\rho}{\rho_0} = \frac{V_0}{V} = \frac{S\Delta x}{S\Delta x \left[1+\frac{\partial \xi}{\partial x} \right]} \]
\[ \frac{\rho}{\rho_0} = \frac{1}{1+\frac{\partial \xi}{\partial x} } = 1-\frac{\partial \xi}{\partial x} \;\to\; -\frac{\partial \xi}{\partial x} = \frac{\rho-\rho_0}{\rho_0} = \frac{\Delta\rho}{\rho_0} \]
ou
\[ \frac{V}{V_0} = 1+\frac{\partial \xi}{\partial x} \;\to\; \frac{\partial \xi}{\partial x} = \frac{V-V_0}{V_0} = \frac{\Delta V}{V_0} \]
La description qui prend en compte la géométrie 3D relie linéairement la pression à la variation relative de volume :
$$ p = cste \cdot \frac{\Delta V}{V_0} \;\to\; p = -\frac{1}{\chi} \frac{\Delta V}{V_0} \;\to\; \frac{\Delta V}{V_0} = -\chi p $$
Dans le cas qui nous intéresse, \(\chi\) est la compressibilité adiabatique.
\begin{align*}
\frac{\partial^2 p}{\partial x^2} + \rho \frac{\partial^2}{\partial t^2} \frac{\partial \xi}{\partial x} = 0 & \\
\frac{\partial^2 p}{\partial x^2} + \rho \frac{\partial^2}{\partial t^2}\left[\frac{\Delta V}{V_0} \right] = 0 & \to \frac{\partial^2 p}{\partial x^2} -{\chi\rho}\frac{\partial^2 p}{\partial t^2} = 0
\end{align*}
Le vide (comme les matériaux) possède des propriétés électromagnétiques) !
Trig functions (sine, cosine) are solution to d'Alembert's equation.
In the form :
$$\xi(x,t)= A\cos(kx \pm \omega t+ \phi ) $$
with : \(\displaystyle c=\frac{\omega}{k}\)
Vérification :
\begin{align*}
\frac{\partial}{\partial t}\left[ \frac{\partial }{\partial t} A \cos(\omega t - kx + \varphi) \right]
- c^2\frac{\partial}{\partial x}\left[\frac{\partial }{\partial x}A\cos(\omega t - kx + \varphi)\right] &= 0 \\
\frac{\partial}{\partial t}\left[-\omega A\sin(\omega t - kx + \varphi)\right] - c^2\frac{\partial}{\partial x}\left[kA\sin(\omega t - kx + \varphi)\right] &= 0 \\
-\omega^2 A\cos(\omega t - kx + \varphi) + c^2k^2A\cos(\omega t - kx + \varphi) &= 0
\;\to\; c=\frac{\omega}{k}
\end{align*}
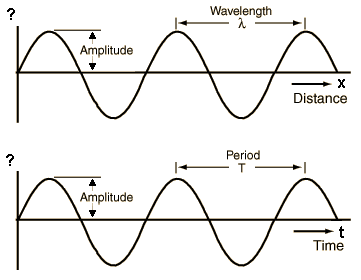
Space (\(\lambda\)) and time (\(T\)) periodicity are explicited :
$$\cos\left(2\pi\left(\frac{x}{\lambda} \pm \frac{t}{T}\right)+ \phi \right )$$
$$k=\frac{2\pi}{\lambda} \; ; \; \omega = 2\pi f = \frac{2\pi}{T} \quad\to \quad c=f\lambda$$
The EM field \(E(x,t)\)is written in complex notation :
\begin{align*}
E=A\cos(kx \pm \omega t + \phi) & = \Re\left\{\tilde E = Ae ^{j(kx \pm \omega t + \phi)}\right\} \\
& = \Re\left\{\tilde E = Ae ^{j\phi}e ^{j(kx \pm \omega t)}\right\} \\
& = \Re\left\{\tilde E =\tilde Ae ^{j(kx \pm \omega t)}\right\}
\end{align*}
Note: Physical (measurable) quantites can only be expressed with real numbers.
Cette approche fonctionne tant que l'on s'en tient à des opérations linéaires :
$$\Re\{ a z_1 + z_2\} = a \Re z_1 + \Re z_2 $$
$$ \Re\{ z'\} = (\Re z )' $$
mais :
$$\Re\{ z_1 \times z_2\} \neq \Re z_1 \times \Re z_2 $$
For example, a sound wave :
$$f=1000\,{\rm Hz} \; ;\; c=330\,{\rm m.s^{-1}} \quad\to\; \lambda = 0,33\,\textrm{m}$$
Un "point" correspondant à une "phase en particulier" \(\varphi_0\) se propage le long de l'axe \(Oz\) à la vitesse (célérité) \(c\).
En 2D (ou 3D) le lieu, courbe (ou surface), de "même phase" est appelé front d'onde
Le vecteur d'onde indique la direction et sens de propagation de l'onde.
Pour l'onde "localement plane" :
$$ \vec k\cdot \vec r = \rm{cst} $$
$$\frac{\partial}{\partial z}\left[-\frac{1}{\chi}\frac{\Delta V}{V_0}\right]+\rho\frac{\partial^2 \xi}{\partial t^2} = \underbrace{0 = \frac{\partial}{\partial z}\left[\frac{\partial \xi}{\partial z}\right]-\chi\rho\frac{\partial^2 \xi}{\partial t^2}}_{\textrm{équation de d'Alembert}}$$
On peut aussi établir l’équation pour décrire l’évolution spatio-temporelle de la vitesse de déplacement de la perturbation :
$$u(z,t) = \frac{\partial \xi}{\partial t} \quad\to\quad \frac{\partial p}{\partial z} + \rho \frac{\partial^2\xi}{\partial t^2} = 0 = \frac{\partial p}{\partial z} + \rho \frac{\partial u}{\partial t}$$
$$\frac{\partial}{\partial z}\left[-\frac{1}{\chi}\frac{\Delta V}{V_0}\right]+\rho\frac{\partial u}{\partial t} = 0 = \frac{\partial}{\partial z}\left[\frac{\partial \xi}{\partial z}\right]-\chi\rho\frac{\partial u}{\partial t}$$
$$\frac{\partial^2}{\partial z^2}\frac{\partial \xi}{\partial t}-\chi\rho\frac{\partial^2 u}{\partial t^2} = \underbrace{0 = \frac{\partial^2 u}{\partial z^2}-\chi\rho\frac{\partial^2 u}{\partial t^2}}_{\textrm{équation de d'Alembert}}$$
La dépendance spatio-temporelle des trois quantité déplacement, vitesse et pression
est déterminée par l'équation de d'Alemebert. Les trois sont décrites par des ondes (ayant la
même célérité).
A partir des solution trigonométriques :
$$ \tilde p = P_0 e^{j(\omega t -kz)} \quad \tilde u = U_0 e^{j(\omega t -kz)} $$
et du P.F.D. :
$$ \frac{\partial p}{\partial z} + \rho \frac{\partial^2\xi}{\partial t^2} = \frac{\partial p}{\partial z} + \rho \frac{\partial u}{\partial t} = 0 $$
$$ -jk P_0 e^{j(\omega t -kz)} = -\rho j\omega U_0 e^{j(\omega t -kz)} \quad\to\; P_0=\rho c U_0 $$
La vitesse est un vecteur.
ou encore :
$$ \tilde u = U_0 e^{j(\omega t \mathbf{+} kz)} $$
On appelle impédance caractéristique, \(Z\), le rapport entre la pression en un point
à un instant donné \(p(z,t)\) et la vitesse (en valeur absolue) en ce même point
au même instant \(u(z,t)\) :
$$ p = \rho c u = Zu $$
Cette impédance décrit la « résistance » qu’un milieu oppose à sa mise en mouvement
lorsqu’il est traversé par une une onde acoustique.
Elle ne dépend que des propriétés mécaniques du milieu :
$$ Z = \rho c = \rho \frac{1}{\sqrt{\chi \rho}} = \sqrt{\frac{\rho}{\chi}}$$
encore ici attention au sens de propagation
L'énergie totale transportée par l'onde acoustique correspond à la somme de l'énergie cinétique et de l'énergie potentielle
L'énergie cinétique est définie à partir de la vitesse locale des "particules" :
$$ E_c = \frac{1}{2}m u ^2 = \frac{1}{2}V_0 \rho u ^2$$
L’énergie potentielle est celle emmagasinée (ou libérée) par la compression
(la dilatation) du milieu. A partir du théorème de l’énergie cinétique :
$$ dE_p = -\vec F \cdot d\vec z = -pSdz = - pdV \;\to\; E_p = -\int_{V_0}^V pdV $$
Élasticité :
$$ \frac{\Delta V}{V_0} = -\chi p \;\to\; \Delta V = -V_0\chi p \;\to\; dV = - V_0\chi dp $$
et donc :
$$ E_p = -\int_{V_0}^V pdV = V_0\chi \int_{V_0}^V pdp = \frac{1}{2}V_0 \chi p ^2 $$
enfin :
$$ E = \frac{1}{2}V_0 \left[\rho u^2 + \chi p ^2\right] $$
Énergie totale par unité de volume :
$$ e = \frac{E}{V_0} = \frac{1}{2} \left[\rho u^2 + chi p^2\right] \, \textrm{J.m}^{-3} $$
avec la définition de l'impédance caractéristique :
$$ p = Zu = \sqrt{\frac{\rho}{\chi}} = \rho c u $$
L’intensité acoustique est le taux moyen d’énergie
(la valeur moyenne de l’énergie par unité de temps) traversant une surface unitaire
(S=1m\(^{2}\) perpendiculaire à la direction de propagation :
$$ [I] = \frac{[E]}{[T][L^2]} = J.s^{-1}.m^{-2} = W. m^{-2} $$
$$ \underbrace{dW = F d\xi}_{E = \textrm{travail}} \;\to\; \frac{dW}{S} = p d\xi \;\to\; \frac{dW}{Sdt} = p \frac{d\xi }{dt} = pu $$
donc :
$$ I = \langle pu \rangle = \frac{1}{T}\int_0^T p(z,t)u(z,t)dt $$
Comme il s’agit d’une opération nonlinéaire, il faut utiliser la notation réelle :
$$ I = P_0U_0 \underbrace{\frac{1}{T} \int_0^T \cos^2(\omega t -kz) dt}_{\frac{1}{2}} = \frac{P_0U_0}{2} $$
avec la définition de l'impédance caractéristique :
$$ I = \frac{P_0U_0}{2} = \frac{P_0^2}{2Z} = \frac{ZU_0^2}{2}$$
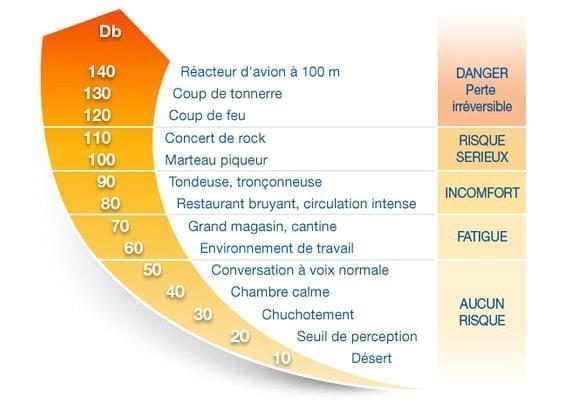
L’oreille est sensible à une large gamme de pressions acoustiques (d’intensités acoustiques).
On utilise une échelle logarithmique : le décibel
Pression :
$$\displaystyle p_i+p_r = p_t $$
Flux :
\begin{align*}
\vec J_i + \vec J_r = \vec J_t \quad\to\quad & S_1\vec u_i + S_1\vec u_r = S_2\vec u_t \\
& S_1 u_i - S_1 u_r = S_2 u_t \\
& S_1 \frac{p_i}{Z_1} - S_1 \frac{p_r}{Z_1} = S_2 \frac{p_t}{Z_2}
\end{align*}
Pour la pression :
interface entre deux matériaux différents : \(Z_1 \neq Z_2\) et \(S_1 = S_2\)
interface entre deux matériaux identiques : \(Z_1 = Z_2\) et \(S_1 \neq S_2\)
Pour l'intensité acoustique :
inteface entre deux matériaux différents : \(Z_1 \neq Z_2\) et \(S_1 = S_2\)
On constate que l'énergie est bien conservée :
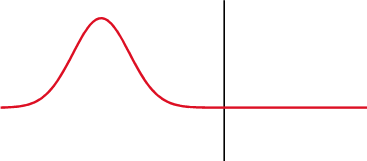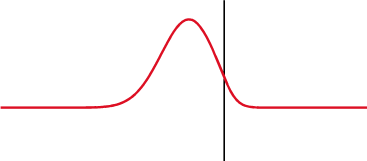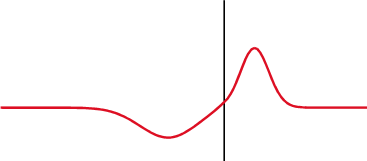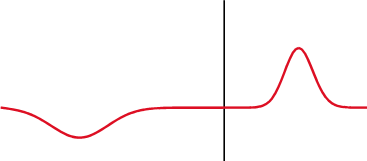
Remarquez l'effet de la parité de la fonction !
Formule d'Euler :
\begin{align*}
f(t) &= a_0 + \sum_n a_n \sin n\omega t + \sum_n b_n \cos n\omega t \\
&= a_0 + \sum_n a_n \frac{e^{in\omega t}-e^{-in\omega t}}{2i} + b_n \frac{e^{in\omega t}+e^{-in\omega t}}{2} \\
&= a_0 + \sum_n \frac{b_n-ia_n}{2}e^{in\omega t} + \frac{b_n+ia_n}{2}e^{-in\omega t} \\
&= a_0 + \sum_n c_n e^{in\omega t} + c_n^* e^{-in\omega t}
\end{align*}
Série complexe, fréquences "négatives"
$$f(t)=\sum_{n=-\infty}^{\infty} c_n e^{in\omega t} \quad ;\; c_n=\frac{1}{T}\int_0^T f(t) e^{-in\omega t}dt \quad ;\; c_n^* = c_{-n} $$
On définit la transformée de Fourier (TF), notée \(X(f)\), d'un signal \(x(t)\) et son inverse comme suit :
\[ TF\{x(t)\} \equiv X(f) = \int_{-\infty}^\infty x(t)e^{-j2\pi ft} dt\]
\[ TF^{-1}\{X(f)\} \equiv x(t) = \int_{-\infty}^\infty X(f)e^{+j2\pi ft} df\]
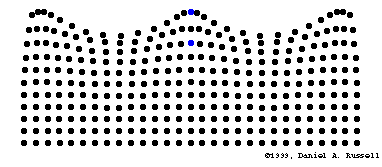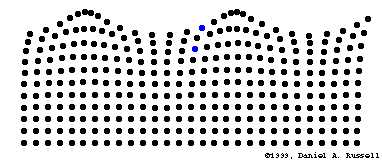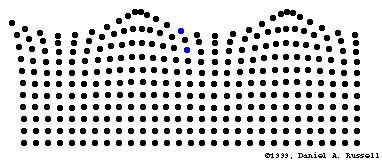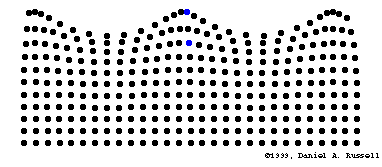
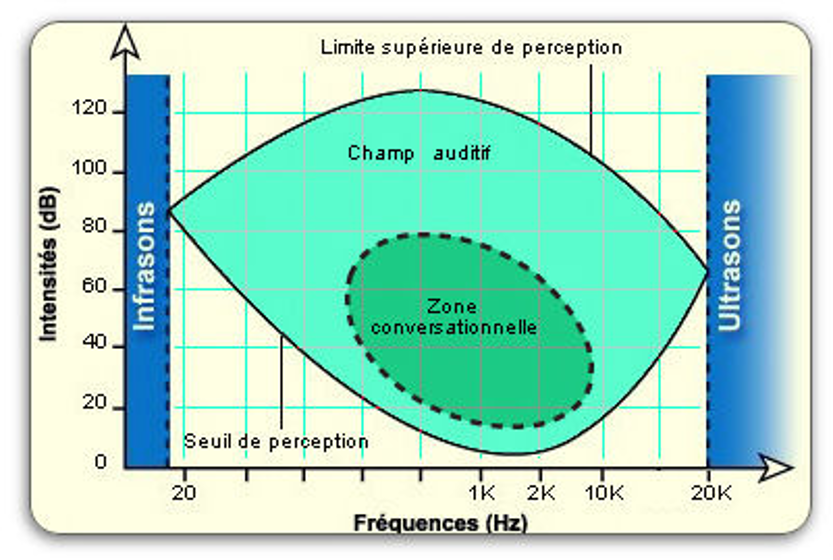
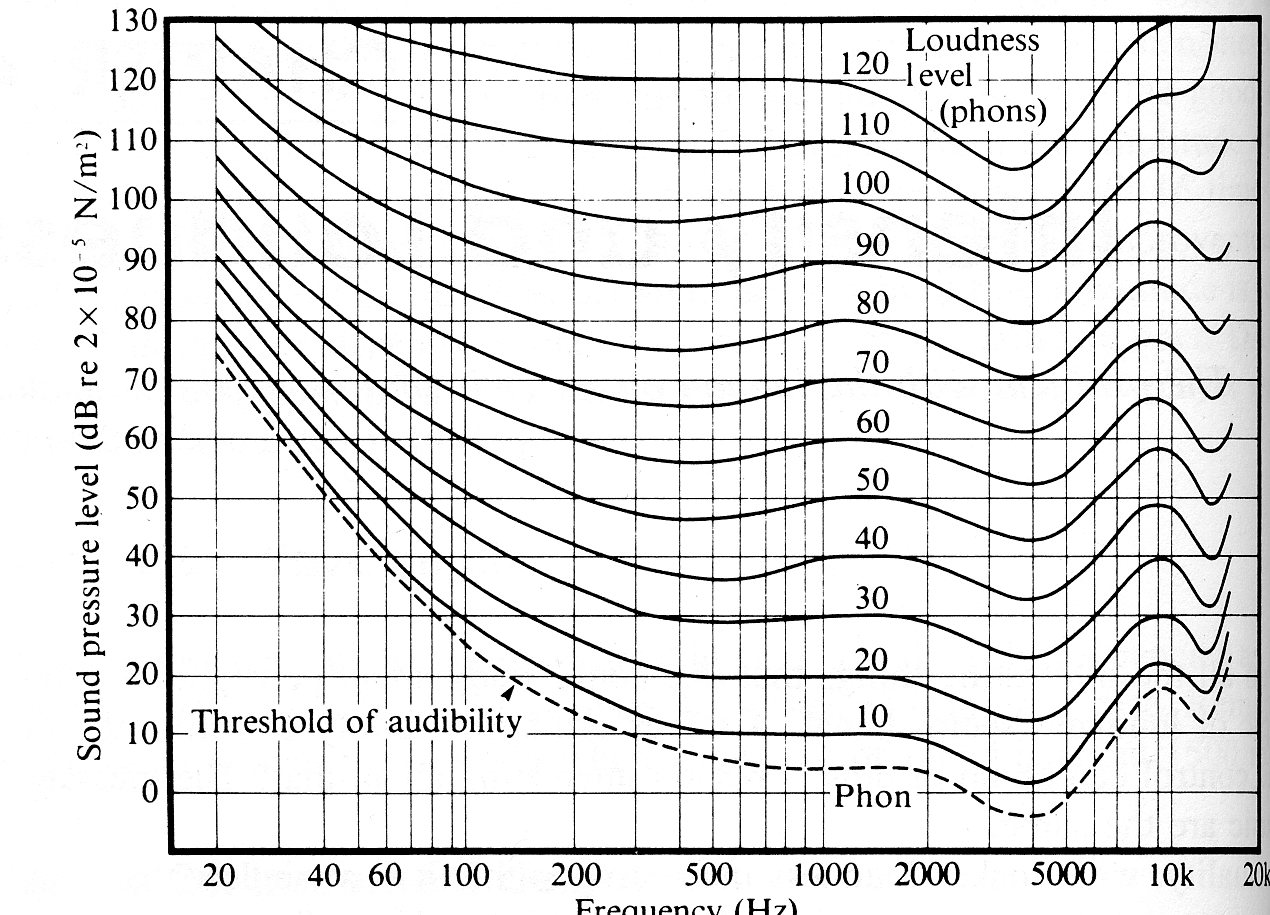
L'oreille externe agit comme un résonateur (amplificateur)
Le phone est l'unité du niveau acoutisque perçu d'un son pur. Elle permet de comparer deux sons de fréquences différentes :
Quelle que soit l’échelle de perception de perception utilisée on obtient une relation monotone en fonction de l’intensité acoustique
De combien doit-on augmenter l'intensité acoustique pour "doubler" l'impression sonore ?
Attention :
Transport d'énergie sans transport de matière

Description mathématique
\[ \xi(x,t) = \xi(x-ct) \qquad\left\{\xi(x+ct)\;\textrm{si}\; \vec c= -c \vec u_x \right\} \]
Vu par le mathématicien

Vu par la physicien
la corde vibrante
Vu par le physicien
onde de pression dans un tuyau
Démonstration : Dynamique
On définit :
Conservation de la masse
$$ V_0 = S \Delta x $$
\begin{align*}
V &= S\left[ \Delta x + \xi(x+\Delta x) - \xi(x)\right] \\ &= S\Delta x\left[1+\frac{\partial \xi}{\partial x}\right]
\end{align*}
Élasticité : Loi de Hooke
$$F=k\Delta \ell$$
Ondes électromagnétiques ?
 \begin{align}
\vec \nabla \cdot \vec E &= \frac{\rho}{\varepsilon_0} \\
\vec \nabla \cdot \vec B &= 0 \\
\vec \nabla \times \vec E &= -\frac{\partial\vec B}{\partial t} \\
\vec \nabla \times \vec B &= \mu_0 \vec j + \mu_0\varepsilon_0\frac{\partial\vec E}{\partial t} \\
\end{align}
\begin{align}
\vec \nabla \cdot \vec E &= \frac{\rho}{\varepsilon_0} \\
\vec \nabla \cdot \vec B &= 0 \\
\vec \nabla \times \vec E &= -\frac{\partial\vec B}{\partial t} \\
\vec \nabla \times \vec B &= \mu_0 \vec j + \mu_0\varepsilon_0\frac{\partial\vec E}{\partial t} \\
\end{align}
 $$-\nabla^2 \vec E +\mu_0\varepsilon_0 \frac{\partial^2 \vec E}{\partial t^2} = 0$$
$$ c=\frac{1}{\sqrt{\mu_0\varepsilon_0}} $$
$$-\nabla^2 \vec E +\mu_0\varepsilon_0 \frac{\partial^2 \vec E}{\partial t^2} = 0$$
$$ c=\frac{1}{\sqrt{\mu_0\varepsilon_0}} $$
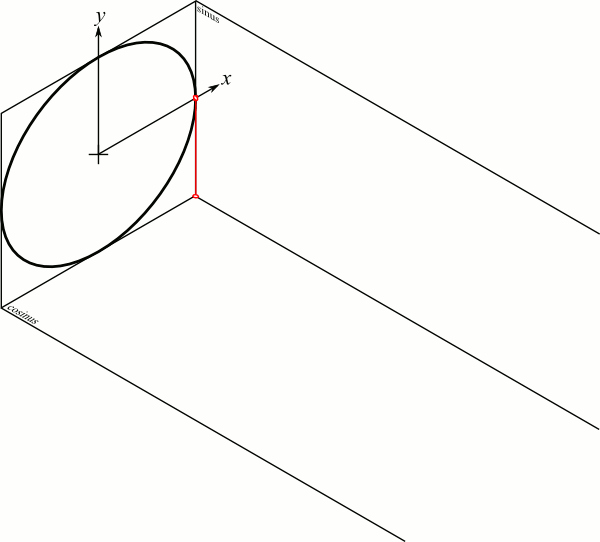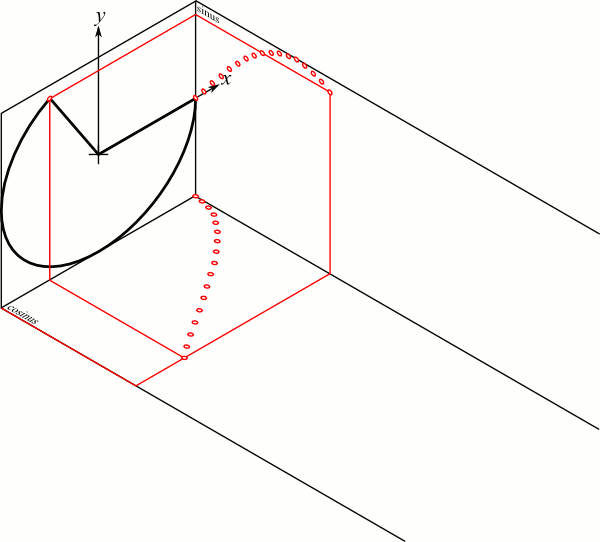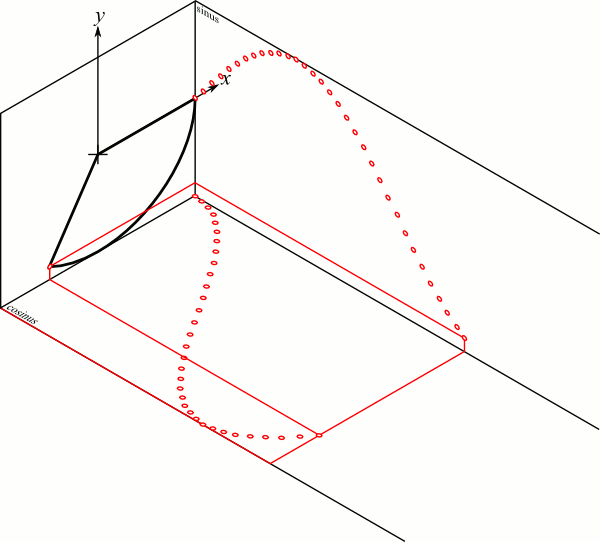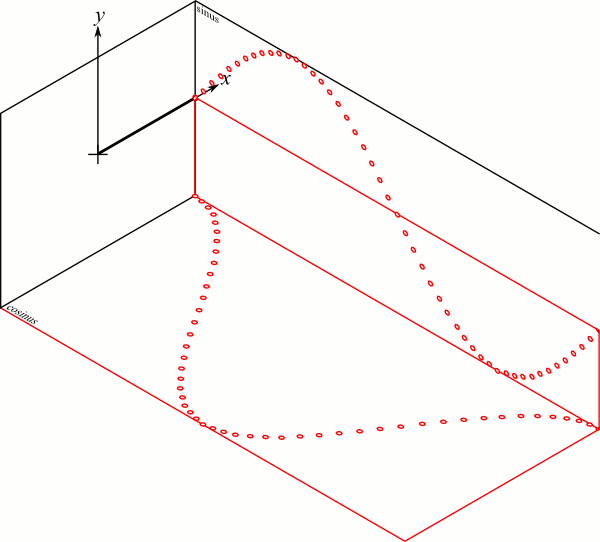
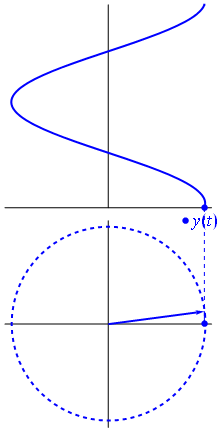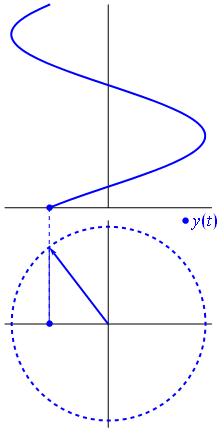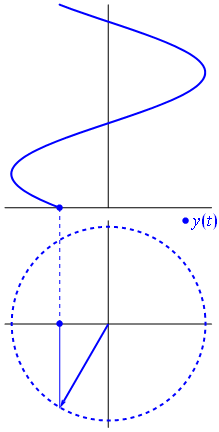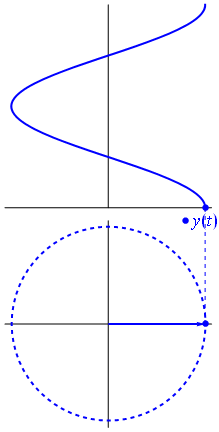
Fonctions trigonométriques
Onde en notation complexe
Attention au caractère linéaire
Amplitude et Phase
Onde plane propagative
$$\tilde{E}=\tilde{A}e^{j( \omega t \pm kr)}$$
 https://commons.wikimedia.org/w/index.php?curid=31381808
https://commons.wikimedia.org/w/index.php?curid=31381808
Onde propagative : "phaseur"
\begin{align}
\omega t -kw &= \varphi_0 \\
x &= \frac{\varphi_0}{k}+\frac{\omega}{k}t \\
&= \frac{\varphi_0}{k}+ct
\end{align}
Ondes en 2 et 3 dimensions

Vecteur d'onde
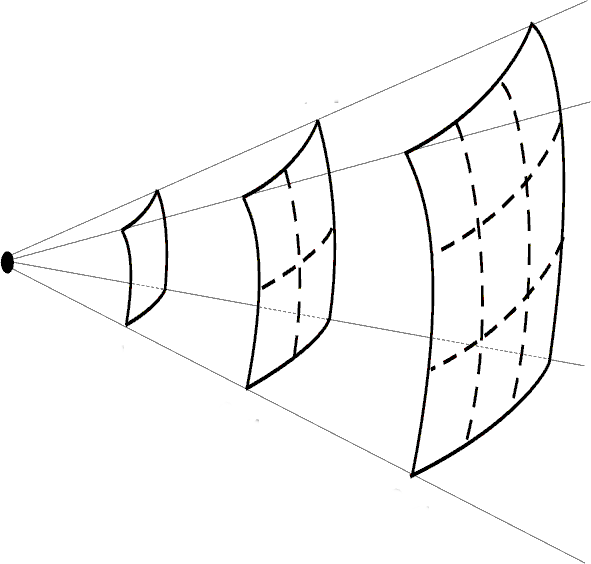

$$ \vec k\cdot \vec r = {\rm cst} \quad\to \quad \tilde{E}=\tilde{A}e^{j( \omega t \pm \vec k \cdot \vec r)}$$
Energie
Onde "de déplacement"
Onde "de vitesse"
Relation pression vitesse
Sens de propagation
Dans notre description à une dimension le changement de sens du vecteur correspond
à un changement de signe.
Impédance caractéristique
Énergie
Densité totale d'énergie
$$ e = \frac{1}{2} \left[\rho u^2 + chi p^2\right] = \chi p^2 = \rho u^2 = \frac{pu}{c} $$
Intensité acoustique
Niveau Sonore en dB
Transmision et reflexion
Continuïté à l'interface : pression et flux
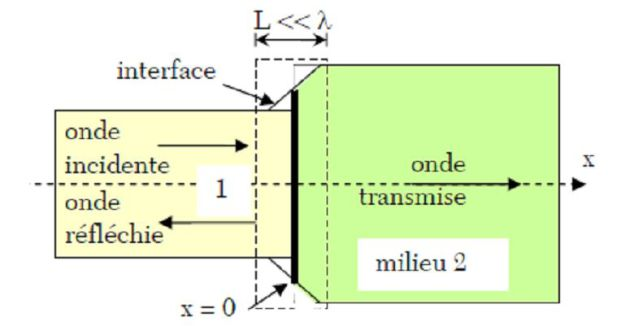
Coefficient de réflexion et transmission
$$
\left.
\begin{array}{l}
p_i + rp_i = tp_i \\
\frac{p_i}{Z_1} - r \frac{p_i}{Z_1} = t \frac{p_i}{Z_2}
\end{array}
\right\}
\to\quad
\left.
\begin{array}{l}
1 + r = t \\
\frac{1-r}{Z_1} = \frac{t}{Z_2}
\end{array}
\right\}
\to\quad
\begin{array}{l}
r = \frac{Z_2-Z_1}{Z_2+Z_1} \\
t = \frac{2Z_2}{Z_2+Z_1}
\end{array}
$$
$$
\left.
\begin{array}{l}
p_i + rp_i = tp_i \\
S_1 p_i - r S_1 p_i = t S_2 p_i
\end{array}
\right\}
\to\quad
\left.
\begin{array}{l}
1 + r = t \\
S_1 (1-r) = S_2 t
\end{array}
\right\}
\to\quad
\begin{array}{l}
r = \frac{S_1-S_2}{S_2+S_1} \\
t = \frac{2S_1}{S_2+S_1}
\end{array}
$$
$$ I = \frac{p^2}{2Z} $$
$$
I_r = R I_i \quad \to \quad \frac{r^2 p_i^2}{2Z_1} = R \frac{ p_i^2}{2Z_1} \quad \to \quad R = r^2
$$
$$
I_t = T I_i \quad \to \quad \frac{t^2 p_i^2}{2Z_2} = T \frac{ p_i^2}{2Z_1} \quad \to \quad T = \frac{Z_1}{Z_2}t^2
$$
$$ R + T = \frac{Z_2^2 + Z_1^2 - 2Z_1Z_2}{(Z_2+Z_1)^2} + \frac{4Z_1Z_2}{(Z_2+Z_1)^2} = 1$$
Ondes stationnaires
Oreille capteur de son
Physiologie de l'oreille
Rôle de l'oreille moyenne
Son simple, son complexe, son musical
Représentation spectrale
Série et transformée de Fourier
Espaces vectoriels, Espaces de Hilbert : Analogie
Signal "Carré"




Représentation spectrale












en complexes
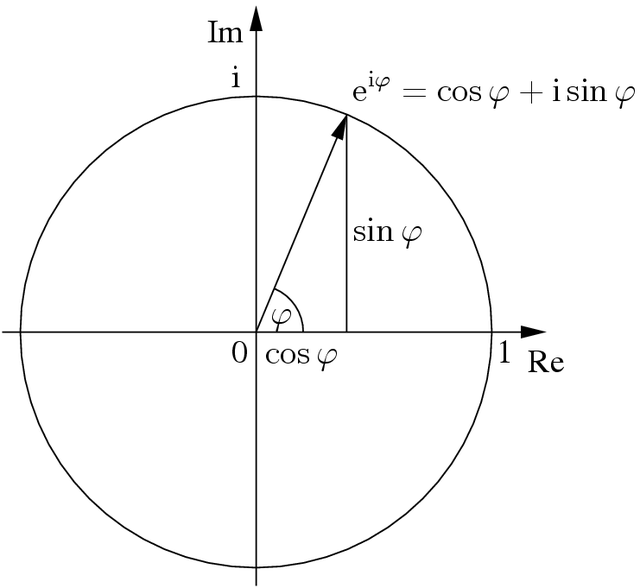
$$ e^{i\theta}=\cos\theta +i\sin\theta \quad\to\quad \cos\theta = \frac{e^{i\theta}+e^{-i\theta}}{2} \; ;\; \sin\theta = \frac{e^{i\theta}-e^{-i\theta}}{2i}$$






Transformée de Fourier
Ondes acoustiques
Son simple, son complexe, son musical
oreille interne : analyse spectrale
Intensité acoustique vs Sonie
Intensité et Perception


Intensité et fréquence : "phone"
1 phone = Intensité acoustique de 1 dB @ 1 kHZ
Psychoacoustique
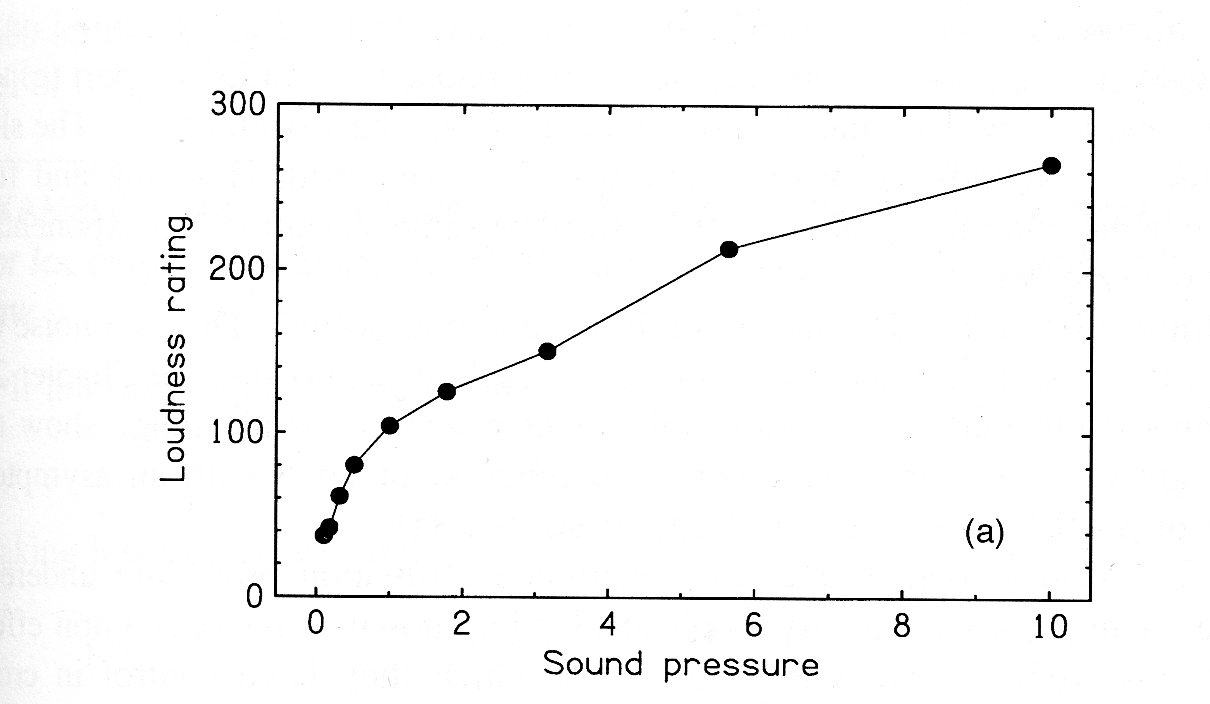 $$ \Psi=kI^p$$
$$ \Psi=kI^p$$
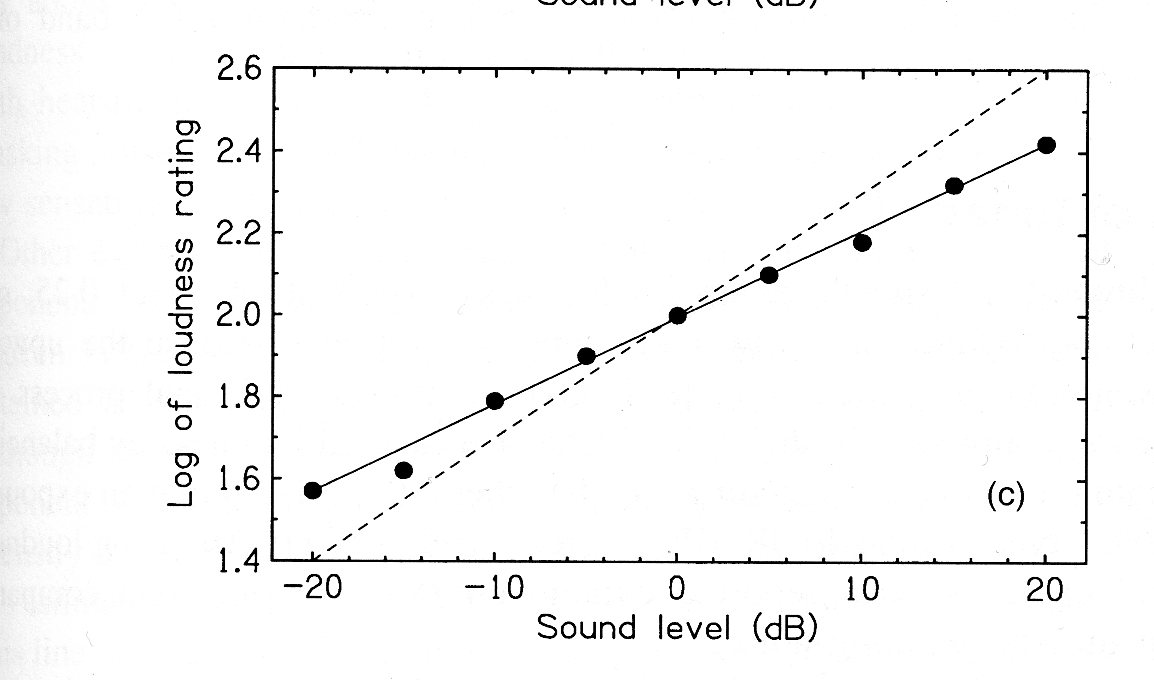 $$ \log_{10}\Psi=\log_{10}k + p \log_{10} I$$
$$ I_{dB}=10\log_{10}\frac{I}{I_{ref}} $$
$$ \log_{10}\Psi = \log_{10}kI_{ref}^p +p\frac{I_{dB}}{10}$$
$$ \log_{10}\Psi=\log_{10}k + p \log_{10} I$$
$$ I_{dB}=10\log_{10}\frac{I}{I_{ref}} $$
$$ \log_{10}\Psi = \log_{10}kI_{ref}^p +p\frac{I_{dB}}{10}$$
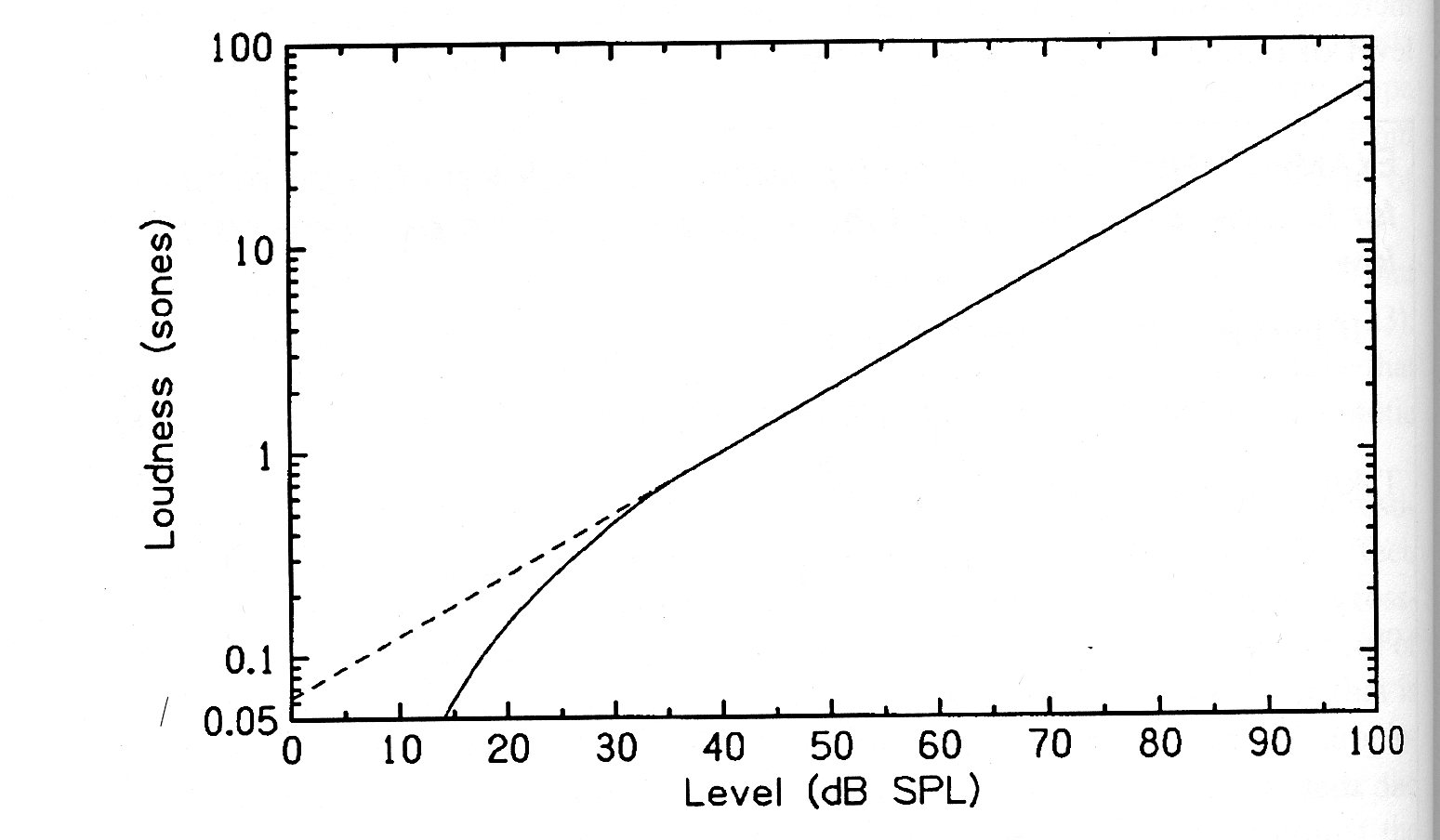
Sones
$$\Psi_{(sone)}=\frac{1}{15,849}\left(\frac{I}{I_{ref}}\right)^{0,3} \quad\to\quad \log_{10}\Psi_{(sone)}=-1,2+0,03I_{dB}$$
| Source sonore | Pression acoustique | Niveau de pression | Volume |
|---|---|---|---|
| pascal | dB re 20 µPa | sone | |
| Seuil de la douleur | 100 | 134 | ~ 676 |
| Dommages à court terme | 20 | approx. 120 | ~ 250 |
| Jet, 100 m distant | 6 - 200 | 110 - 140 | ~ 125 - 1024 |
| Marteau-piqueur, à 1 m / discothèque | 2 | approx. 100 | ~ 60 |
| Dommages à long terme | 6×10−1 | approx. 90 | ~ 32 |
| Route majeure, à 10 m | 2×10−1 - 6×10−1 | 80 - 90 | ~ 16 - 32 |
| Voiture, à 10 m | 2×10−2 - 2×10−1 | 60 - 80 | ~ 4 - 16 |
| Téléviseur à volume normal, à 1 m | 2×10−2 | ca. 60 | ~ 4 |
| Discussion normale, à 1 m distant | 2×10−3 - 2×10−2 | 40 - 60 | ~ 1 - 4 |
| Pièce très calme | 2×10−4 - 6×10−4 | 20 - 30 | ~ 0.15 - 0.4 |
| Brise, respiration calme | 6×10−5 | 10 | ~ 0.02 |
| Seuil d'audibilité à 2 kHz | 2×10−5 | 0 | 0 |
Loi de Stevens / Loi de Weber-Fechner
L'idée d'utiliser une loi de puissance a été popularisée par S. Stevens,
on peut la considérer comme une "variante de la loi de Weber-Fechner.
On considère que la différence de perception se mesure en nombre de seuils de différence \(\Delta I\) : $$d\Psi=\frac{dI}{\Delta I} $$
et que ce seuil de différence est proportionnel à l'intensité : $$\Delta I = kI$$
$$ \Psi = \int_0^\Psi d\Psi'= \int_{I_0}^I\frac{dI'}{\Delta I} = \frac{1}{k}\int_{I_0}^I\frac{dI'}{I'}= \frac{\ln 10}{k}\log_{10}\frac{I}{I_{0}}$$On trouve une loi logarithmique plutôt qu'une loi de puissance.
... mais l'expérience ne confirme pas l'hypothèse \(\Delta I = kI\)
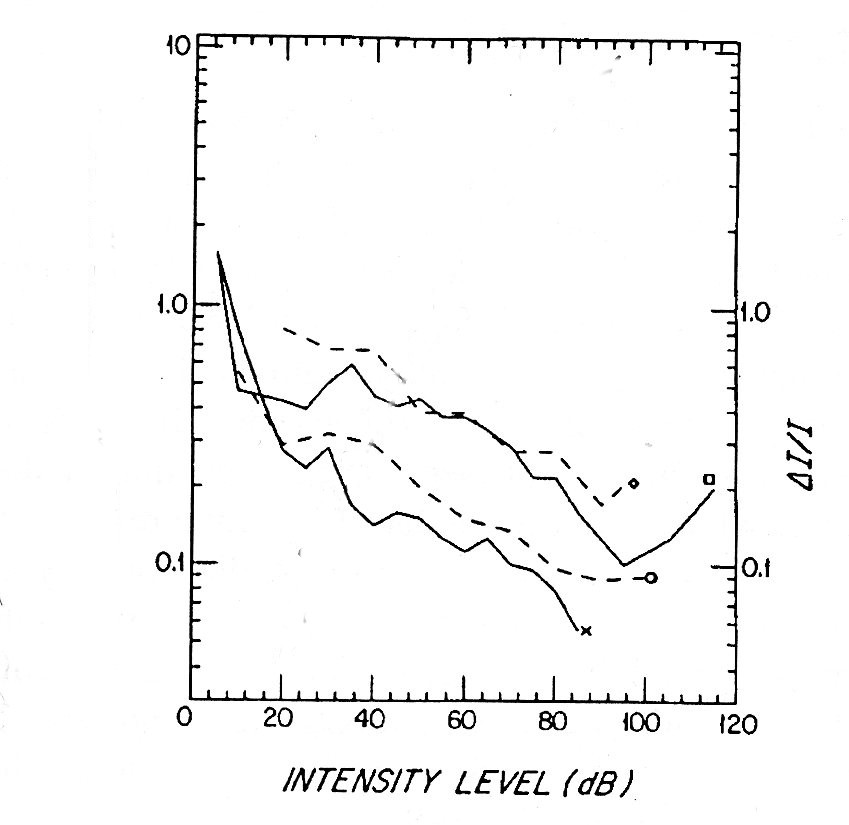
Potentiels d'actions
On propose de relier l'unité de sensation au taux de potentiels d'actions déclenchés \(R\) : $$ \Psi = aR -b$$
Même si on ne connaît pas la fonction \(R(I)\), on peut supposer qu'il s'agit d'une fonction continue dérivable. En utilisant la technique de la différentielle : $$ \Delta R = \frac{dR}{dI}\Delta I$$
Enfin, on peut considérer \(R\) comme une variable aléatoire, décrite par une statistique de Poisson : $$ \Delta R = c\sqrt{R} \;\to\; \frac{dR}{\sqrt{R}}=c\frac{dI}{\Delta I}$$
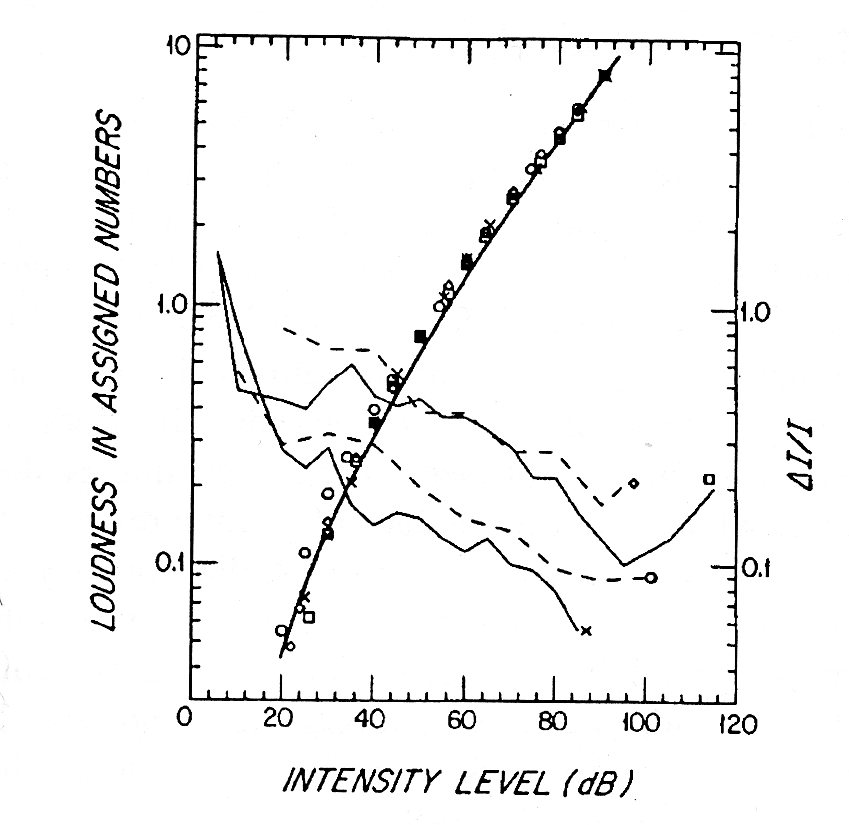
L'accord est assez bon.
On retrouve le comportement en loi de puissance pour \(I_{dB}>30dB\).
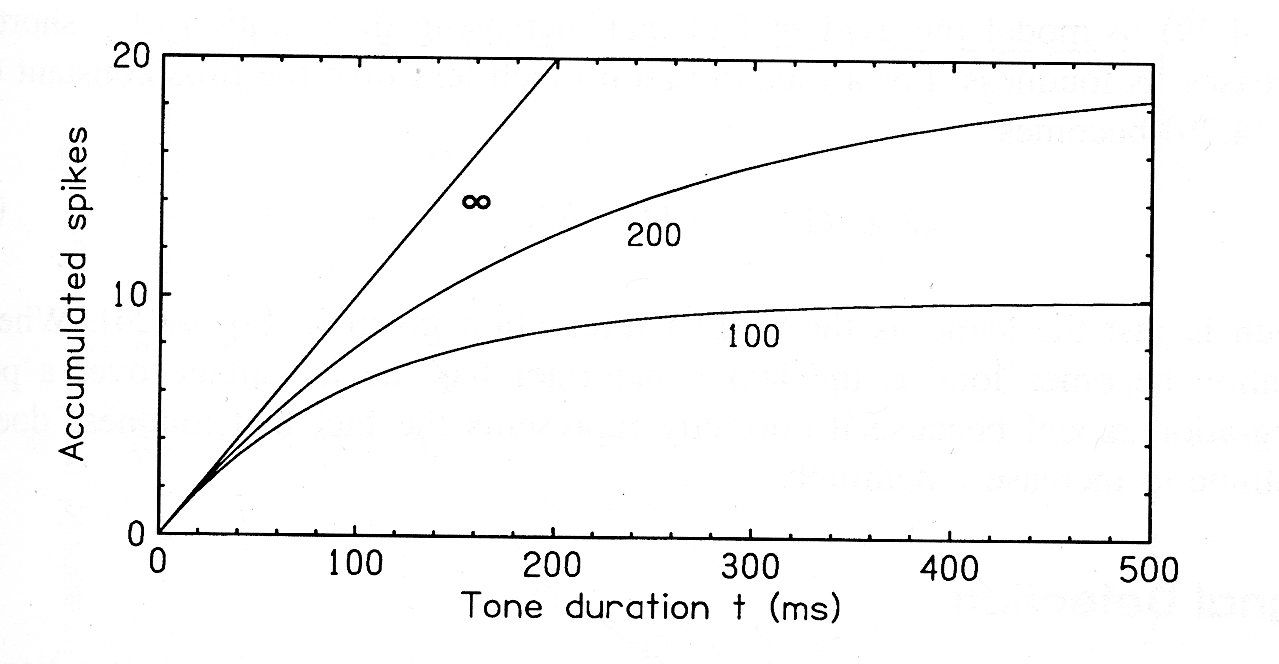
Intensité et durée
Modèle de l'intégrateur à fuite
$$ h=Rt \;\to\; \frac{dh}{dt}=R-l \;\to\; \frac{dh}{dt}=R-\frac{h}{\tau} \;\to\; Rt\left(1-e^{-t/\tau}\right)-\underbrace{h(0)}_{=0}e^{-t/\tau}$$