Capteurs de déformation, de force, d'accélération
Benoît C. FORGET
2015-2016
Laboratoire neurophotonique
UFR des Scicences Fondamentales et Biomédicales
benoit.forget@parisdescartes.fr
Généralités
Deux types de capteurs :
- "qualitatifs" ou détecteur de seuil (e.g. un bouton);
- "quantitaifs" : qui associe une grandeur numérique à la mesure.
Deux principes de mesure de force :
- mesure de la déformation d'un matériau soumis à une force ;
- mesure direct par un phénomène physique dépendant de la force appliquée.
Effet Piézo-résistif
$$R=\rho\frac{4\ell}{\pi D^2}$$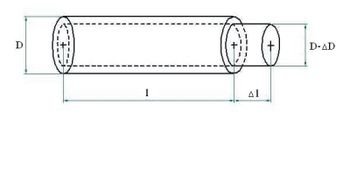 $$\frac{\Delta L}{L} \; ;\; \frac{\Delta D}{D} \; ; \ldots \; \to \; \frac{\Delta R}{R} $$
$$\frac{\Delta L}{L} \; ;\; \frac{\Delta D}{D} \; ; \ldots \; \to \; \frac{\Delta R}{R} $$
Déformation des matériaux
On s'intéresse à :
- la déformation élastique est une déformation réversible ;
- L'élasticité linéaire concerne les petites déformations.
Limites de l'élasticité
- rupture pour le matériaux dits "fragiles"
- déformation plastique (irréversible et non-linéaire) pour les matériaux "ductiles"
- éventuellement le fluage (surtout à température élevée)
Relation force-déformation
On cherche des relations linéaires entre la force appliquée et la déformation
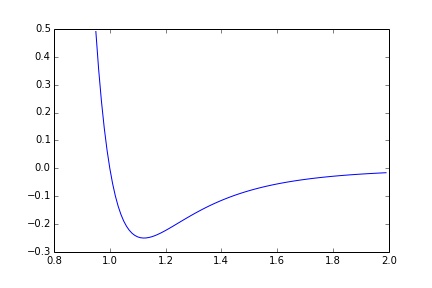
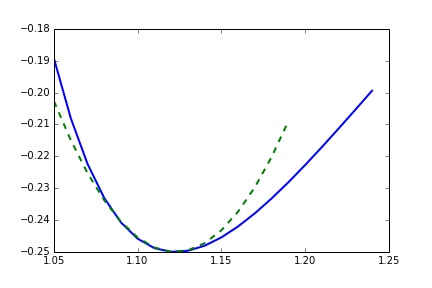
Aspect énergétique
$$E_p(x) \approx E_p(x_{eq}) + (x-x_{eq})\left. \frac{dE_p}{dx}\right|_{x_{eq}} + \frac{(x-x_{eq})^2}{2}\left. \frac{d^2E_p}{dx^2}\right|_{x_{eq}} $$
\(x_{eq}\) étant une position d'équilibre : \(\displaystyle \left. \frac{dE_p}{dx}\right|_{x_{eq}} = 0\)
\(x_{eq}\) étant une position d'équilibre stable : \(\displaystyle \left. \frac{d^2E_p}{dx^2}\right|_{x_{eq}}\equiv k > 0\)
$$ E_p(x) \approx E_p(x_{eq}) + \frac{1}{2}k(x-x_{eq})^2$$
Force de rappel élastique
A partir de la relation entre travail et énergie potentielle :
$$ \vec F = - \vec\nabla E_p \quad\to\quad F_x(x)=-\frac{dE_p}{dx}$$ $$ E_p(x) \approx E_p(x_{eq}) + \frac{1}{2}k(x-x_{eq})^2 \quad\to\quad F_x(x)=-k(x-x_{eq})$$Au voisinage de\(x_{eq}\) le système se comporte comme un oscillateur harmonique si il est soumis à une force de rappel élastique
Loi de Hooke

régime statique
Loi de Hooke : \(\vec F_h=-k\vec x\)
$$ \sum\vec F = m\vec g - k\left(x - \ell\right) \vec e_x = m \vec a = m\frac{d^2x}{dt^2} $$longueur à l'équilibre \(\ell_0\) : $$ m\frac{d^2x}{dt^2} = 0 \quad\to\quad \ell_0 = \ell + \frac{mg}{k} $$
régime dynamique
On perturbe le système en déplaçant la masse (on crée une entrée, une excitation) : $$ m\frac{d^2x}{dt^2} = -k\underbrace{(x-\ell_0)}_{X \textrm{ : allongement}} $$
$$ m\frac{d^2X}{dt^2} = - k X \quad\to\quad \frac{d^2X}{dt^2} + \omega_0 X = 0$$
avec \(\displaystyle \omega_0^2=\sqrt{\frac{k}{m}}\).
$$ X= X_m \cos \left(\omega_0 t + \phi\right)$$ \(X_m\) et \(\phi\) sont déterminés par les conditions initiales du problème.
Oscillateur harmonique amorti
On considère en plus une force de frottement proportionnelle (et de sens opposé) à la vitesse $$\vec F_f = - \gamma \frac{\partial x}{\partial t} \; ; \gamma > 0 $$
$$m\frac{\partial^2 x}{\partial t^2} + \gamma \frac{\partial x}{\partial t} + kx = 0 \quad\to\quad \frac{\partial^2 x}{\partial t^2} + \frac{1}{\tau} \frac{\partial x}{\partial t} + \omega_0^2x = 0 $$
- \(\displaystyle \omega_0=\sqrt{\frac{k}{m}}\) : résonance. \(\displaystyle [\omega_0]=\sqrt{\frac{[MT^{-1}]}{[M]}}=[T^{-1}]\)
- \(\displaystyle \tau = \frac{m}{\gamma}\) : temps caratctéristique. \(\displaystyle [\tau]=\frac{[M]}{[MT^{-1}]}=[T]\)
- \(Q=\omega_0\tau\) : facteur de qualité. \([Q]=[T^{-1}T]=[]\)
- \(\displaystyle \zeta=\frac{1}{2Q} \) : facteur d'amortissement. \(\displaystyle [\zeta]= \frac{1}{[Q]}=[]\)
action d'une force extérieure
$$ F_{ext}(t) = F_0\cos(\omega_e t + \varphi_e) $$$$\frac{\partial^2 x}{\partial t^2} + \frac{1}{\tau} \frac{\partial x}{\partial t} + \omega_0^2x = \frac{F_0}{m}\cos(\omega_e t + \varphi_e) $$
Il y a superposition de deux régimes :
- Le régime transitoire caractérisé par la solution générale de l'équation sans second membre (apériodique, pseudopériodique, critique)
- Le régime permanent caractérisé par la solution particulière, qui sera de la forme : $$ x(t)=x_0\cos(\omega_e t+\varphi) $$
régime permanent
En notation complexe :
$$ x(t) = \Re\left\{\tilde x(t) \right\} \quad ;\quad F_{ext}(t) = \Re\left\{\tilde F_{ext}(t) \right\} $$
$$ \tilde F_{ext}(t) = F_0e^{i(\omega_e t+\varphi_e)}= F_0e^{i\varphi_e} e^{i\omega_e t}= \tilde F_0e^{i\omega_e t}$$
$$\frac{\partial^2 \tilde x}{\partial t^2} + \frac{1}{\tau} \frac{\partial \tilde x}{\partial t} + \omega_0^2 \tilde x = \frac{\tilde F_0}{m}e^{i\omega_e t} $$
La solution particulière est de la forme :
$$\tilde x(t)= \tilde x_0 e^{i\omega_e t} \quad\to\quad \left[(i\omega_e)^2 + i\frac{\omega_e}{\tau} + \omega_0^2\right] \tilde x_0 e^{i\omega_e t} =\frac{\tilde F_0}{m}e^{i\omega_e t} $$
La solution est donc :
$$ \tilde x_0=\frac{\tilde F_0}{m\left[(\omega_0^2-\omega_e^2) + i\frac{\omega_e}{\tau}\right]}$$
réponse du système
$$ \tilde x_0 = \tilde R \tilde F_0 \quad \to\quad \tilde R = \frac{1}{m\left[(\omega_0^2-\omega_e^2) + i\frac{\omega_e}{\tau}\right]} = \rho e^{i\theta}$$$$ \tilde x(t) = \tilde x_0 e^{i\omega_e t} = \rho e^{i\theta} F_0 e^{i\varphi_e} e^{i\omega_e t}\quad\to\quad x(t) = \rho F_0 \cos (\omega_e t+\varphi_e +\theta)$$
La réponse est caractérisée par l'amplitude \(\rho F_0\) et la phase \(\theta\) :
$$ \rho (\omega_e)= \frac{1}{m\sqrt{(\omega_0^2-\omega_e^2)^2 + \left(\frac{\omega_e}{\tau}\right)^2}} \quad ;\quad \tan\theta = -\frac{\omega_e}{\tau(\omega_0^2-\omega_e^2)} $$
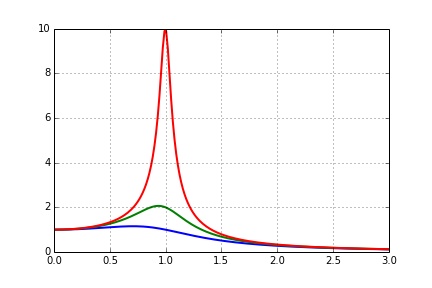
3D
module d'Young, coef. de Poisson
Déformation selon \(x\) : $$ \epsilon_x = \frac{\Delta \ell}{\ell} \; \to \; \sigma_x=E\epsilon_x$$
Déformation selon \(y\) : $$ \epsilon_y = \frac{\Delta d}{d} \; \to \; \epsilon_y=-\nu\epsilon_x$$
Jauge de contrainte
$$R=\rho\frac{\ell}{S} \; \to \; \frac{\Delta R}{R}= f\left(\frac{\Delta \ell}{\ell}\right)$$
Pour un cylindre de longueur \(\ell\) et de diamètre \(D\) :
$$ R= \frac{4\rho \ell}{\pi D^2} \; \to\; dR=\frac{4 \ell}{\pi D^2}d\rho+\frac{4 \rho}{\pi D^2}d\ell-\frac{8\rho \ell}{\pi D^3}dD $$
$$ \frac{dR}{R}= \frac{d\rho}{\rho}+\frac{d\ell}{\ell}-2\frac{dD}{D}$$
$$ K=\frac{dR/R}{d\ell/\ell}= \frac{d\rho/\rho}{d\ell/\ell}+1-2\frac{dD/D}{d\ell/\ell} = 1+2\nu + \frac{d\rho/\rho}{d\ell/\ell}$$
Relation entre \(\Delta R\) et la force \(F\)
$$ F=\sigma s = Es\frac{d\ell}{\ell}$$$$ F = \frac{Es}{K}\frac{dR}{R} \quad \frac{dR}{R}=\frac{K}{Es}F$$
\(K\) est le facteur de jauge.
\(K\approx 2-4\) pour les métaux, \(\pm 50 < K <\pm 200 \) pour les semiconducteurs.
Coefficient de température
$$ K=K_0\left[1+\alpha_k\Delta T\right]$$$$ \frac{\Delta R}{R}=K_0\left[1+\alpha_k\Delta T\right]\frac{d\ell}{\ell} $$
$$ \Delta R = K_0\left[1+\alpha_k\Delta T\right]R_0[1+\alpha_R\Delta T]\frac{d\ell}{\ell}$$
Étude de cas
Accéléromètre piézo résistif
I. Principe de base du capteur
On considère la structure de la figure ci-dessous réalisée en silicium micro-usiné où une masse sismique centrale est suspendue à un bâti par quatre poutres flexibles identiques de masses négligeables.
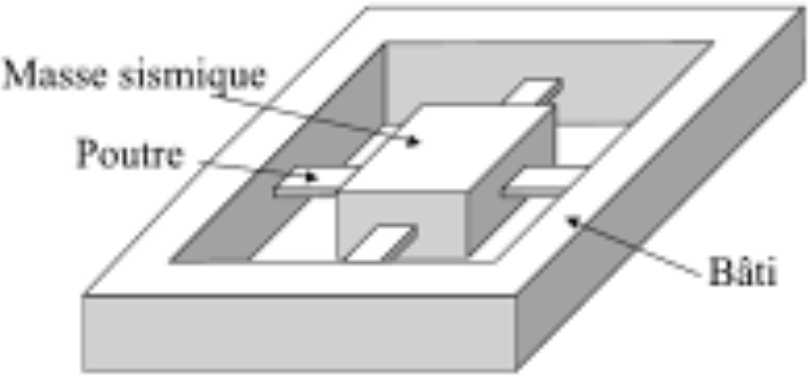
Considérons deux poutres de même axe. Soient \(L\) la longueur de ces poutres et \(\vec P\) le poids de la masse sismique. Tout se passe comme si ce couple de poutres était soumis à la force \(\vec F = \vec P/2\) ; le reste du poids étant supporté par l’autre couple de poutres.
D’un point de vue Résistance des Matériaux, ceci est équivalent à une poutre unique de longueur double \(2L\) se déformant sous l’action de la force \(\vec F = \vec P/2\) appliquée en son milieu.
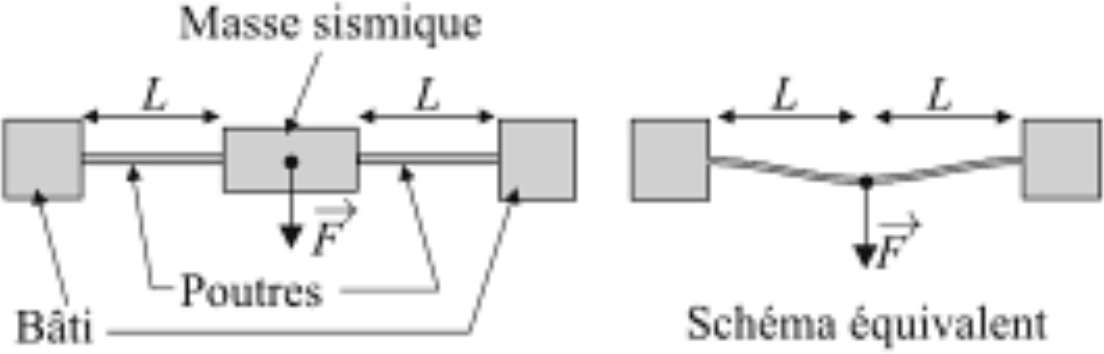
Sous l’action de la force appliquée, une distribution de contraintes prend naissance dans les poutres déformées \(\sigma_{yy}\).

Chaque poutre est de largeur \(\ell\) (direction Ox), de longueur \(L\) (direction Oy) et d’épaisseur \(e\) (direction Oz). On montre qu’en tous les points d’une section droite de la poutre (parallèle au plan xOz) située à une distance \(y\) de l’encastrement dans le bâti, la contrainte \(\sigma_{yy}\) est donnée par : $$\sigma_{yy} = \frac{zM_f}{I}$$ où \(M_f\) est le moment de flexion et \(I\) le moment quadratique de la section droite par rapport à son axe médian parallèle à l’axe Ox.
On donne : $$M_f = F (L − 2y)/4$$ pour \(0 \leq y \leq L\) où \(F\) représente le module de \(\vec F\).
Et : $$I=\frac{\ell e^3}{12}$$
On se propose de mesurer l’accélération subie par la masse sismique, ici l’accélération de la pesanteur, en diffusant sur chacune des poutres des jauges de contrainte alors situées à la surface des poutres. Sur la face supérieure de chaque poutre, on diffuse deux jauges de contrainte alignées sur la direction Oy de la longueur de la poutre : une à proximité du bâti (indice +) et une à proximité de la masse sismique (indice −).

1. Donner la déformation \(\epsilon_{//}\) dans la direction \(y\), à la surface des poutres. On note \(E\) le module d’Young du matériau des poutres.
2. Afin de rester dans le domaine élastique, on fixe la déformation maximale à \(\epsilon_{max}= 2.10^{−3}\). Au maximum, le système doit pouvoir supporter une accélération totale de \(\pm 5g\) selon la direction \(z\) où \(g\) est l’accélération de la pesanteur. Calculer les valeurs maximales de la masse \(m\) et du volume \(v\) de la masse sismique pour rester en-deçà de la limite fixée. On donne \(L = 500 μm\), \(\ell = 20 μm\), \(e = 1 μm\), \(E = 140 kN/mm^2\), \(g = 10 m.s^{−2}\) et la masse volumique du silicium \(d = 2,33 g/cm^3\).
3. Les jauges sont de longueur \(\ell_j\). Montrer que la déformation moyenne d’une jauge centrée à la distance \(y_0\) du bâti est égale à la déformation au point \(y_0\) . On négligera l’effet lié à l’épaisseur de la jauge.
4. Déterminer, en première approximation, la distance au bâti à laquelle doivent être implantées les jauges de contrainte puis les déformations correspondantes \(\epsilon_+\) et \(\epsilon_-\).
5. Les quatre poutres sont équipées de la même façon. Les deux jauges proches du bâti (jauges +) de deux poutres dans le même alignement sont connectées en série pour former la résistance \(R_1\) et les deux jauges proches de la masse sismique (jauges −) constituent en série la résistance \(R_2\). On procède de la même façon avec les deux poutres perpendiculaires aux précédentes pour former respectivement les résistances \(R_3\) (jauges +) et \(R_4\) (jauges −). Donner les expressions des résistances \(R_1\), \(R_2\), \(R_3\) et \(R_4\) sachant que leur valeur au repos est \(R\) et leur coefficient de jauge \(K\).
6. Les résistances ainsi constituées sont montées en pont. Celui-ci est alimenté par une source de tension continue \(V_g\)
d’impédance interne négligeable.

Donner l’expression de la tension de mesure \(V_{mes}\) en fonction de \(R_1\), \(R_2\), \(R_3\) et \(R_4\) puis
de \(K\), \(R\) et \(\epsilon\). Conclure.
II. Effet de la température
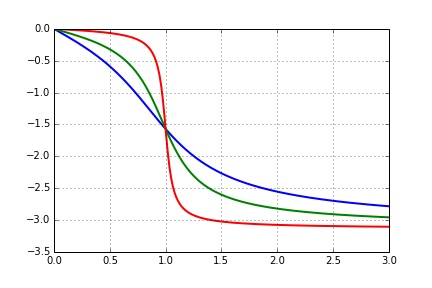
Les jauges sont réalisées par diffusion de dopant P sur la structure de silicium dopé N. La résistance au repos et le facteur de jauge dépendent tous les deux de la température. Dans la plage de température d’utilisation du capteur, les valeurs des coefficients de température correspondants sont données par les courbes de la figure ci-dessous.

7. Déterminer la valeur de la concentration à adopter pour que la variation de la résistance d’une jauge sous l’action de la contrainte soit, au premier ordre, indépendante de la température. On notera \(R_0\) et \(K_0\) respectivement les valeurs de la résistance au repos et du facteur de jauge à la température \(T_0 = 0^\circ\) C.
8. La condition précédente étant réalisée pour la valeur la plus élevée de la concentration, montrer que la mesure dépend de la température au travers de la résistance des jauges au repos.
9. Pour compenser cette dérive, on introduit entre l’alimentation et le pont un dipôle de compensation quasiment linéaire avec la température. Celui-ci est constitué d’une CTN en parallèle avec une résistance fixe et dont la résistance dans la plage d’évolution de la température est correctement approchée par \(R_c = R_{c0} (1+\alpha_c T)\). Ce dipôle est réalisé en couche mince sur le bâti de façon à être à la même température que les jauges. Montrer qu’un réglage judicieux de la valeur des caractéristiques de ce dipôle permet d’annuler l’effet thermique sur la tension de mesure. Pour la suite, on note \(R_0 + R_{c0} = \beta R_0\).
III. Comportement statique
10. On montre que la flèche maximale prise par les poutres (c’est-à-dire le déplacement selon \(z\) de leur extrémité en \(y = L\)) est donnée à l’équilibre par : $$ z(L) = − \frac{FL^3}{2Ele^3} $$ En remarquant que \(z(G) = z(L) = z_{max}\) où \(G\) est le centre de gravité de la masse sismique, montrer qu’à l’équilibre la réaction des poutres sur la masse sismique peut s’écrire comme la force de rappel d’un ressort de raideur \(k\) dont on donnera l’expression en fonction de \(E\), \(\ell\), \(e\) et \(L\).
11. La masse \(M\) du bâti étant très supérieure à la masse sismique, calculer la pulsation propre \(\omega_0\) du système en fonction de \(k\) et \(m\).
12. Écrire, dans l’approximation linéaire, la tension de mesure du pont de la figure 14.5 en fonction de la position \(z(G)\). Montrer que l’on peut écrire \(V_{mes} = Az(G)\) et calculer la tension de mesure si la masse sismique n’est soumise qu’à son propre poids. On donne \(V_g = 10 V\), \(K_0=45\), \(\beta = 1,2\) et on considère que \(\ell_j << L\).
V. Comportement dynamique
13. La masse sismique est maintenant soumise en plus de son poids à une accélération extérieure \(a\). On montre de plus que l’amortissement du mouvement est du type fluide (force \(−λz\)) et est essentiellement dû à l’air environnant la masse sismique. Établir l’équation différentielle en \(z\) du centre de gravité de la masse sismique en fonction de \(m\), \(k\), \(λ\), \(a\) et \(g\).
14. Donner l’expression de la fonction de transfert en régime harmonique \(H(j\omega)\) = \(V_{mes}/(g + a)\) en introduisant la fréquence propre et le coefficient d’amortissement \(\zeta\).
15. Donner l’expression de la sensibilité S(ω) en fonction de \(A\), \(\omega\), \(\omega_0\) et \(\zeta\).
16. On suppose que l’on se trouve à l’amortissement critique, \(\zeta=1\). Donner la nouvelle expression de la sensibilité.
17. Calculer \(S(0)\) et \(S(\omega_0)\).
18. Calculer la fréquence de coupure à 1% \(f_{1}\) de cet accéléromètre.
19. En l’état, quelle fragilité présente cet accéléromètre et comment y remédier ?
Capteur capacitifs
Capteurs piézoélectriques
