Capteurs de rayonnement lumineux
Benoît C. FORGET
2015-2016
Laboratoire neurophotonique
UFR des Scicences Fondamentales et Biomédicales
benoit.forget@parisdescartes.fr
Capteurs de lumière
- Propriétés fondamentales
- Absorption, longueur d'onde, photon
- Notions de photométrie
- Sources lumineuses
- Grandeurs métrologiques propres aux capteurs optiques
- Cellule Photoconductrice
- Photodiode
Absorption, longueur d'onde, photon
Génération de photons
Soit un matériau dont le coefficient de réflexion (en puissance) est \(R\) soumis à un rayonnement lumineux de \(\Phi\) watt :
- le nombre \(n_i\) de photons incidents par seconde est : $$n_i=\frac{\Phi}{h\nu}=\lambda\frac{\Phi}{hc}$$
- le nombre \(n_a\) de photons absorbés par seconde est : $$n_a=(1-R)n_i=(1-R)\lambda\frac{\Phi}{hc}$$
- le nombre \(G\) d'électrons (phot-électrons) créés par seconde est : $$G=\eta n_a=\eta (1-R)\lambda\frac{\Phi}{hc}$$ où \(\eta\) est le rendement quantique : le nombre d'électrons (ou de trous) créés pour l'absorption d'un photon.
Effets photoélectriques
Selon la nature du dispositif éclairé, l'effet photoélectrique se manifeste sous diverses formes :
- photoconduction
- photovoltaïque
- photoémission
- photoélectromagnétique
Notions de photométrie
Les grandeurs relatives aux rayonnements lumineux peuvent être évaluées :
- Abstraction faite de toute notion de perception sensorielle en considérant les grandeurs énergétiques dans les unités "habituelles" de la physique (joule, watt). C'est la radiométrie.
- En "pondérant" cette énergie par la sensation visuelle qu'elle produit. C'est la photométrie visuelle.
Définition des grandeurs radiométriques
On s'intéresse à l'énergie de l'onde lumineuse. On définit :
- Le flux énergértique \(\Phi\) : C'est la quantité d'énergie par unité de temps $$ \Phi = \frac{[\textrm{Energie}]}{[\textrm{temps}]} = \frac{J}{s} = W = {[\textrm{Puissance}]}$$
- L'éclairement \(E\) : C'est le flux énergétique par unité de surface $$ E= \frac{d\Phi}{dS} =\frac{[\textrm{Puissance}]}{[\textrm{Surface}]} = W.m^{-2} $$ Le flux énergétique du soleil sur la Terre est de \(1\, kW.m^{-2}\)
Pour une source ponctuelle, on définit :
- L'intensité énergétique \(I\) C'est le flux énerétique par unité d'angle solide
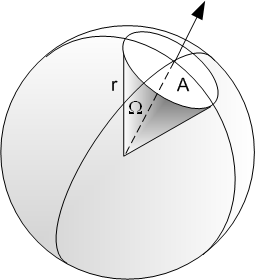
- L'angle solide \(\Omega\) est le rapport entre la surface \(A\) et le rayon \(r\)
- il est exprimé en stéradiant
- la sphère entière correspond à 4\(\pi\) sr
 |
|
rq : comme la lumière se propage "en ligne droite" cette quantité se conserve quelle que soit la distance par rapport à la source (contrairement à l'' éclairement)
Pour une source étendue, on définit:
- la brillance énergétique \(B\) C'est l'intensité énergétique par unité de surface apparente de la source
$$ B = \frac{dI}{d(\sigma \cos\theta)} = \frac{\frac{d\Phi}{d\Omega}}{d\sigma \cos\theta} = \frac{d^2\Phi}{d\Omega d\sigma \cos\theta} = \textrm{W.m}^{-2}.\textrm{sd}^{-1} $$
\(d\sigma \cos\theta\) est l'élément de surface perpendiculaire à la direction de propagation.
Une source dont la luminance énergétique est la même dans toutes les directions satisfait à la loi de Lambert (source lambertienne).
Radiométrie spectrale
Toutes ces grandeurs peuvent être définies pour une source monochromatique ou sur tout le spectre de la source
$$ \Phi_\lambda = \frac{d\Phi}{d\lambda} = \textrm{W.m}^{-1} \quad\to\quad \Phi= \int_0^\infty \Phi_\lambda S(\lambda) d\lambda $$ $$ E_\lambda = \frac{dE}{d\lambda} = \textrm{W.m}^{-3} \quad\to\quad E= \int_0^\infty E_\lambda S(\lambda) d\lambda $$ $$ I_\lambda = \frac{dI}{d\lambda} = \textrm{W.sr}^{-1}.\textrm{m}^{-1} \quad\to\quad I= \int_0^\infty I_\lambda S(\lambda) d\lambda $$ $$ B_\lambda = \frac{dB}{d\lambda} = \textrm{W.sr}^{-1}.\textrm{m}^{-3} \quad\to\quad B= \int_0^\infty B_\lambda S(\lambda) d\lambda $$
Définition des grandeurs photométriques
Grandeurs radiométriques
|
Grandeurs photométriques
|
- Intensité énergétique \(\to\) Intensité lumineuse : candela, \([cd]\)
- Flux énergétique \(\to\) Flux lumineux : lumen, \([lu]\)
- Eclairement énergétique \(\to\) Eclairement lumineux : lux, \([lx]=[lu.m^{-2}]\)
- Brillance énergétique \(\to\) Luminance\([cd.m^{-2}]\)
\(\approx 1\, cd\qquad \approx 120\, cd\)


| Eclairement | \(lx\) | |
|---|---|---|
| ciel nocturne | \(3.10^{-4}\) | |
| pleine lune | \(0,2\) | |
| ampoule 75 W à 2m | \(40\) | |
| éclairage de rue | \(50\) | |
| éclairage artificiel | \(100\) | |
| extérieur, temps clair | \(2.5\,10^{4}\) | |
| plein soleil, midi | \(10^5\) |
| Luminance | \(cd.m^{-2}\) | |
|---|---|---|
| seuil de percep. oeil | \(10^{-6}\) | |
| ciel nocturne | \(10^{-4}\) | |
| pleine lune | \(2.10^{3}\) | |
| papier blanc, au soleil | \(3.10^{4}\) | |
| éblouissment | \(5.10^{5}\) | |
| lésions possibles | \(2.5\,10^{8}\) | |
| soleil | \(1.6\,10^{10}\) |
Défintion du candela
C'est l'unité fondamentale
1 candela c'est :
- l'intensité d'une bougie
- l'intensité dans une direction perpendiculaire à une ouverture de 1/60 \(cm^2\) surface rayonnant comme un radiateur intégral à la température de solidification du platine (2028 K)
- l’intensité lumineuse, dans une direction donnée, d’une source qui émet un rayonnement monochromatique de fréquence égale à 540 \(10^{12}\) Hz et dont l’intensité énergétique dans cette direction est de 1,464 \(10^{-3}\) \(W.sr^{-1}\).
Perception et grandeurs physiques
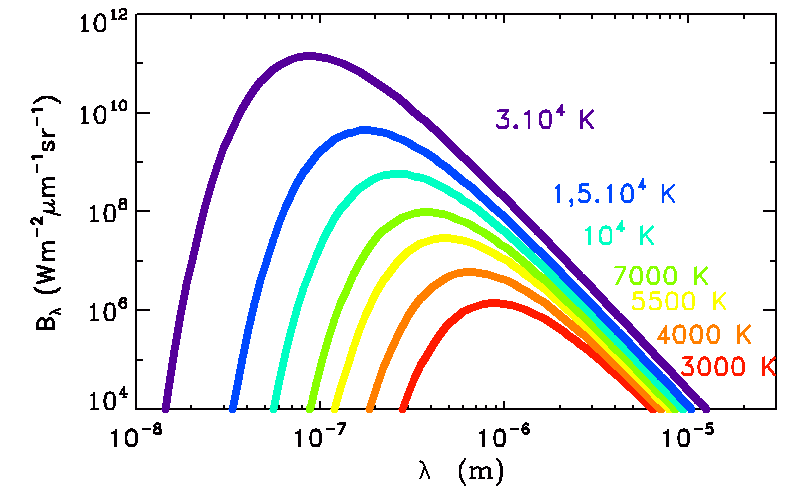
- La sensibilité de l'oeil dépend de la longueur d'onde
- On la définit de façon normalisée : \(0\leq v \leq 1\)
- en vison diurne, elle maximale pour \(\lambda = 555\,\textrm{nm}\) (jaune)
- \(v\) ne dépend pas de \(B\) en première approximation
- La luminance est le produit de la brillance énergétique par la sensibilité de l'oeil $$ L= k\times(vB)$$
- \(k\) est facteur de proportionnalité qui dépend des unités choisies
l’intensité lumineuse, dans une direction donnée, d’une source qui émet un rayonnement monochromatique de fréquence égale à 540 \(10^{12}\) Hz et dont l’intensité énergétique dans cette direction est de 1,464 \(10^{-3}\) \(W.sr^{-1}\). $$ E=\frac{hc}{\lambda}=h\nu \qquad 540\,\textrm{THz} \quad\to\quad 555\,\textrm{nm} \qquad v(\lambda=555\,\textrm{nm})=1$$ $$ L= k\times(vB) \quad\to\quad I_\ell= k\times(vI_e) $$ $$ k(1\times 1,464 10^{-3})=1\,\textrm{cd} \quad\to\quad k=683 $$
Phénomene du Purkinje
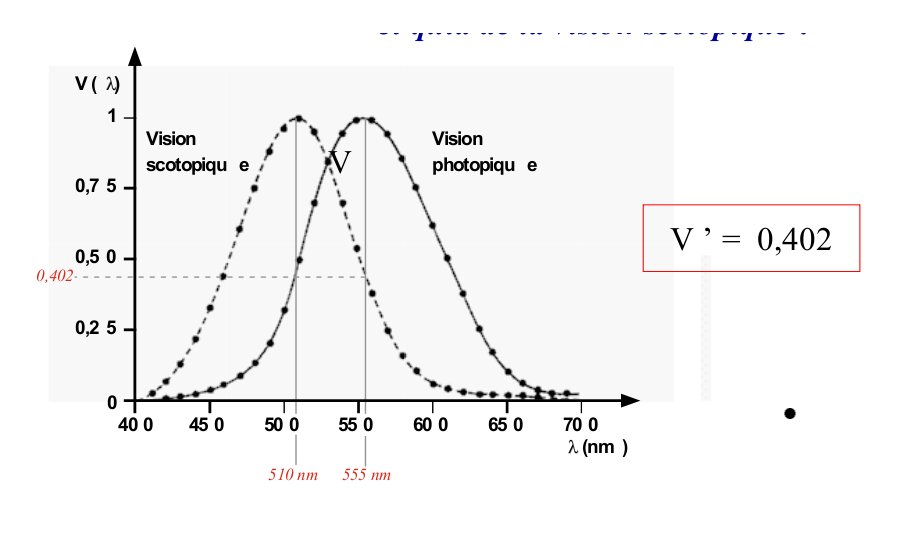 $$k (1\times 1,464\, 10^{-3})=1\,\textrm{cd} \qquad\to k=683$$
$$k' (0,402 \times 1,464 \,10^{-3})=1\,\textrm{cd} \qquad\to k'=1699$$
$$k (1\times 1,464\, 10^{-3})=1\,\textrm{cd} \qquad\to k=683$$
$$k' (0,402 \times 1,464 \,10^{-3})=1\,\textrm{cd} \qquad\to k'=1699$$
Phénomène de Purkinje

Domaines de la vision
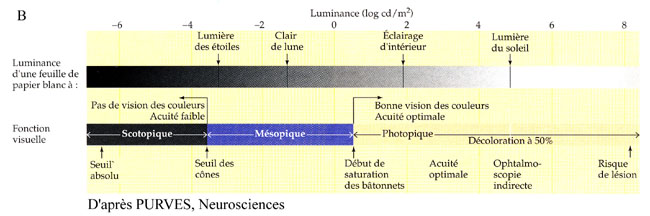
On note :
- Trois “domaines” de vision : scotoptique, mésoptique, photoptique
- L’oeil est sensible sur une très large plage de valeurs de la luminance
Cônes et Batonnets

2 types de cellules photosensibles (vertébrés) :
- Cônes :
- Vision diurne
- Structures spatiales fines
- Vision de couleurs
- Bâtonnets :
- Vision scotoptique
- saturés en vison diurne, ils sont "inutiles"
Sources lumineuses
- Lampe à filament
- Avantages : temps de réponse faible (ns) donc modulation à de fréquences élevées ; fiabilité ; robustesse
- Inconvénients : inertie thermique importante (pas de modulation possible) ; durée de vie limitée
- LED (diode électroluminescente)
- Avantages : flux important ; spectre important (que l'on peut réduire à l'aide de filtres)
- Inconvénients : flux faible (\(\approx 10^{2}\;{\rm mW}\)) ; sensibilité à la température
- laser
- Avantages : monochromatique ; luminance élevée ; très directive ; grande cohérence
Grandeurs métrologiques propres aux capteurs optiques
courant d'obscurité
- C'est un courant permanent délivré par le dispositif lorsque celui-ci est dans l'obscurité.
- Il a pour origine la création de charge par agitation thermique (et/ou absorption d'un rayonnement externe thermique). Il est d'autant plus important pour les détection de photons de faibles énergie (infrarouge)
- On veillera en général à travailler dans des conditions telles que le courant d'obscurité est très faible par rapport à celui produit par le rayonnement que l'on cherche à détecter. Pour les capteur IR ceci implique souvent de les placer dans une enceinte isolante et refroidie
sensibilté
$$I=I_{obs}+I_p$$si le courant d'obscurité est maintenu constant, les fluctuations du courant \(\Delta I\) ne sont dues qu'aux fluctuations du photocourant \(\Delta I_p\).
$$S=\frac{\Delta I}{\Delta \Phi}=\frac{\Delta I_p}{\Delta \Phi}$$L'unité de la sensibilité \(S\) est l'A/W (ou éventuellement l'A/lumen ou l'A/lux)
Pour un capteur linéaire (dont la sensibilité ne dépend pas de \(\Phi\)):
$$S=\frac{I_p}{\Phi}$$sensibilité spectrale
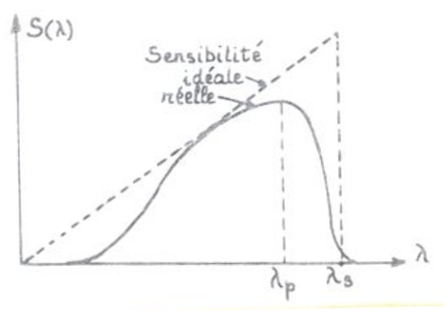
$$S(\lambda)=\frac{\Delta I_p}{\Delta \Phi(\lambda)}\;\to\;\frac{I_p}{\Phi(\lambda)}$$- Pour \(\lambda>\lambda_s\), le photocourant est en principe nul, ainsi donc que la sensibilité ;
- Pour \(\lambda<\lambda_s\), on admettra que le photocourant est proportionnel au nombre \(G\) de photoélectrons créés par seconde $$I\propto G=\frac{\eta(1-R)\lambda}{hc}\Phi \;\to\; S(\lambda)\propto \frac{\eta(1-R)\lambda}{hc}$$
La sensibilité spectrale augmente en fonction de la longueur d'onde, \(S\propto\lambda\).
En fait, \(\eta\) et \(R\) dépendent aussi de \(\lambda\).
bruit et détectivité
C'est la caractéristique du capteur par rapport à son "bruit de fond", sa capacité à détecter des signaux faibles.
Le bruit est représenté par une source de courant dont l'intensité est proportionnelle à la racine carrée de sa valeur quadratique moyenne \(\langle I_b^2\rangle\). Cette VQM dépend des phénomènes physiques en jeu.
pour les capteurs optiques on considère deux types de bruit :
Le bruit d'agitation thermique des porteurs de charge dans toute résistance, pour lequel: $$ \langle I_b^2 \rangle=\frac{4kT B}{R}$$
Le bruit de grenaille (ou bruit quantique ou shot noise) thermique des porteurs de charge dans toute résistance, pour lequel: $$ \langle I_b^2 \rangle=2qIB$$
bruit et bande passante : P.E.B.
Les sources de bruit s'additionnent quadratiquement :
$$ I_b=\sqrt{\sum_i I_{bi}}=i_b\cdot\sqrt{B}$$La bande passante \(B\) est une caractéristique de la mesure (de l'application) plus que du capteur lui-même. C'est la densité spectrale de bruit \(i_b\) qui caractérise le capteur. Elle s'exprime en \(\rm A/\sqrt{Hz}\)
Par définition la puissance équivalente au bruit P.E.B. (noise equivalent power N.E.P.) est la puissance qui produirait en sortie de capteur, pour \(B=1\,{\rm Hz}\) un photocourant \(i_p\) égal au courant de bruit.
$$ i_p=S\cdot P \;\to\; PEB=\frac{i_b}{S}\;{\rm W/\sqrt{Hz}}$$Plus la PEB sera faible, plus le détecteur sera apte à capter des signaux de faible intensité.
detectivité
On définit aussi la détectivité, qui est l'inverse de la PEB :
$$D=\frac{1}{PEB}=\frac{S}{i_b}\;{\rm W^{-1}\cdot\sqrt{Hz}}$$Et comme les bruits élémentaires sont souvent proportionnels à \(\sqrt{A}\) (où \(A\) est la surface active du détecteur) on définit aussi la détectivité spécifique :
$$D^*=\frac{\sqrt{A}}{PEB}= \frac{\sqrt{A}\cdot S}{i_b}=\frac{\sqrt{A}\cdot S\cdot \sqrt{B}}{PEB}\;{\rm cm.\sqrt{Hz}.W^{-1}}$$Cellule photoconductrice
Génération et recombinaison
On considère un semiconducteur "dopé" avec une concentration \(N_d\) d'ions dits "donneurs d'électrons".
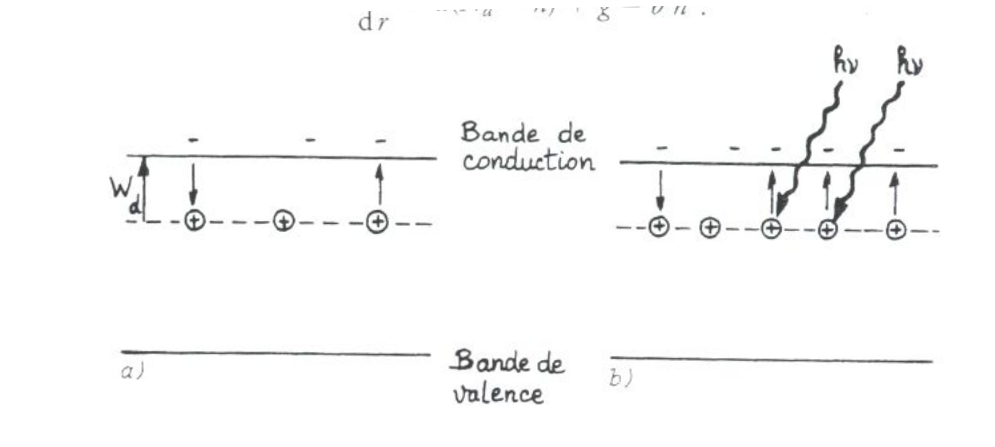
dans l'obscurité
Dans l'obscurité l'ionisation a lieu par activation thermique et elle proportionnelle au nombre de porteurs non-ionisés soit : \(a(N_d-n_o)\) où \(a\propto \exp(-qW_d/kT)\) fixe l'importance de l'activation thermique.
La recombinaison est proportionnelle à la d'électrons \(n_o\) et à celle des atomes ionisés aussi égale à \(n_o\), soit : \(bn_o^2\) $$\frac{d n_o}{d t} = a(N_d-n_o)-bn_o^2 $$
A l'équilibre - régime permanent : $$\frac{d n_o}{d t} = 0 \;\to n_o= -\frac{a}{2b}+\sqrt{\frac{a^2}{4b^2}+\frac{aN_d}{b}} $$
On peut définir la conductivité d'obscurité : $$ \sigma_o=q\mu n_o$$
sous illumination
Sous un flux de photons d'énergie \(> W_d\) des porteurs sont photocréés avec un taux \(G\), ou \(g=G/v\) le taux par unité de volume \(v\) : $$g=\frac{G}{v}=\frac{1}{AL}\frac{\eta(1-R)}{h\nu}\Phi$$
La cinétique de génération-recombinaison devient : $$\frac{d n}{d t} = a(N_d-n)+g-bn^2 $$
On considère le cas où le flux lumineux est assez important pour la photocréation soit le processus dominant et que le nombre de porteurs photocréés soit bien supérieur à celui de poteurs présents dans l'obscurité. $$ g>>a(N_d-n)\; ;\; n>>n_o$$
Dans ces conditions : $$ n=\sqrt{\frac{g}{b}}$$
La conductivité \(\sigma=q\mu n\) est proportionnelle à \(\Phi^{0,5}\). En pratique on trouve \(\sigma\propto\Phi^{0,5 - 1,0}\), ce qui peut être décrit par un modèle plus rigoureux.
notion de "temps de vie"
Le nombre de porteurs se recombinant par est proportionnel au nombre de porteurs \(n\) et inversement proportionnel à leur "temps de vie" \(\tau_n\).
A l'équilibre, ce "taux de recombinaison" est égal au taux de génération : $$ g=\frac{n}{\tau_n}$$
Résistance et "facteur de gain"
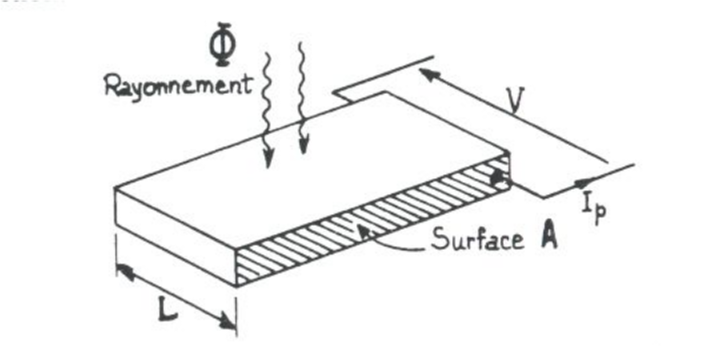
La résistance de la plaque photoconductrice s'exprime comme suit : $$ R=\frac{1}{\sigma}\frac{L}{A}=\frac{1}{q\mu n}\frac{L}{A}$$
Lorsque on applique une ddp \(V\) : $$ I_p = q\mu n \frac{A}{L} V$$
Par ailleurs:
- champ électrique dans la plaque : \(\displaystyle E=\frac{V}{L}\)
- vitesse moyenne des électrons dans le sens du champ : \(u=\mu E\)
- durée du transit des électrons dans la plaque : \(\displaystyle \tau_{tr}=\frac{L}{u}\)
Le courant \(I_p\) est \(F\) fois supérieur à la charge libérée (photocréée) par seconde. \(F\) est un facteur de gain qui peut être de l'ordre de \(10^5\).
On constate que le courant est d'autant plus important que :
- la durée de vie des électrons libres est grandes ;
- la ddp est grande (tant qu'on reste dans le régime ohmique) ;
- la largeur \(L\) de la zone active est faible.
Réalisation d'une cellule photoconductrice
structure en peigne
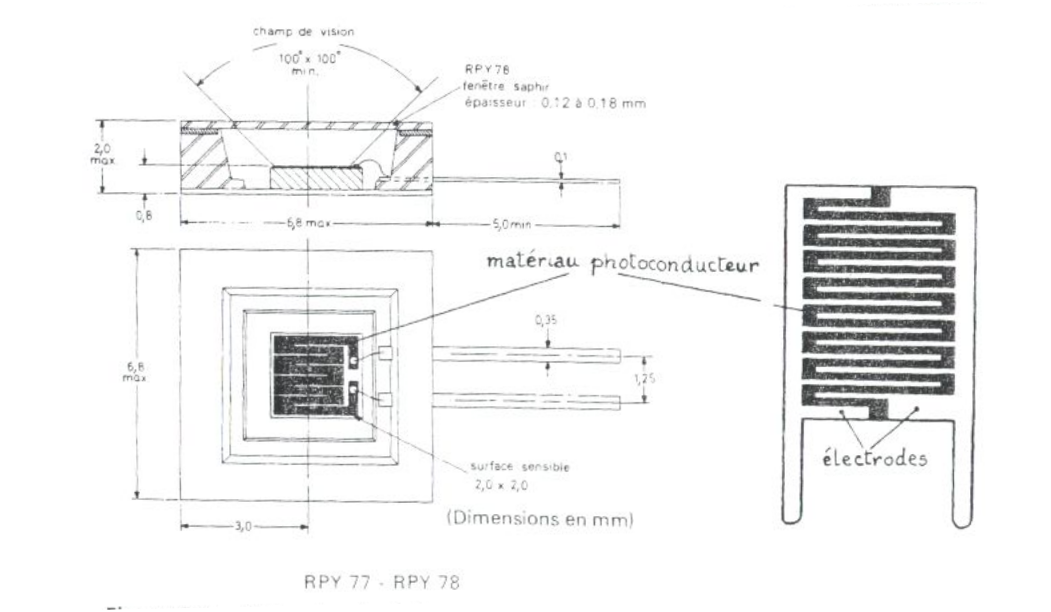
matériaux

Caractéristiques
des cellules photoconductrices
Résistance
On distinguera deux résistances :
- Une résistance d'obscurité \(R_o\), qui dépend du matériau, de la géométrie et de la température. Elle est souvent très élevée (\(10^4 - 10^9 \Omega\])), mais peut être beaucoup plus faible pour certains matériaux (en particulier le CdHgTe )
- La résistance photoélectrique \(R_p=a\Phi^{-\gamma}\).
Ces deux résistances sont en parallèle :
$$R_p//R_o \;\to\; R=\frac{R_oR_p}{R_o+R_p} = \frac{R_oa\Phi^{-\gamma}}{R_o+a\Phi^{-\gamma}} $$En général \(R_o>>R_p \;\to\; R=a\Phi^{-\gamma}\)
La résistance n'est pas linéaire en fonction du flux à mesurer, mais on pourra la linéariser à l'aide d'une résistance fixe, sur une plage flux limitée.
Par ailleurs, il faudra toujours considérer une dépendance en température de la résistance.
Puissance dissipée
Alimentée par une tension \(E\) et une résistance \(R_s\), la puissance dissipée dans la résistance \(P=RI^2=V^2/R\) sera :
$$ P = \frac{RE^2}{(R+R_s)^2}\quad\to\quad P_{max}=\frac{E}{4R_s}\;\textrm{si}\; R_s=R$$C'est l'échauffement liée à cette puissance dissipée qui limite les performances. Un radiateur ou un système de refroidissement est souvent utilisé.
Conductance
On exprime la loi d'Ohm en fonction de la conductance : $$V=RI \;\to\; I=G_cV$$
Ici : $$\frac{1}{R}=\frac{1}{R_o}+\frac{1}{R_p}\;\to\;G=G_{co}+G_{cp}=G_{co}+\frac{\Phi^\gamma}{a}$$
Le courant total s'écrit : $$ I = G_cV = G_{co}V+G_{cp}V = I_o+I_p$$
En général \(I_p >> I_o\): $$ I = I_p= \frac{V}{a}\Phi^\gamma$$
Sensibilité et non linéarité
$$ I = I_p= \frac{V}{a}\Phi^\gamma$$Sauf le cas très particulier où \(\gamma=1\) le courant est une fonction non linéaire du flux reçu
On définira :
- le rapport de transfert statique (ou point de fonctionnement) : \( \displaystyle \frac{I}{\Phi}=\frac{V}{a}\phi^{\gamma-1}\)
- la sensibilité : \( \displaystyle \frac{\Delta I}{\Delta\Phi}=\gamma\frac{V}{a}\phi^{\gamma-1}\)
Remarques
$$ \frac{I}{\Phi}=\frac{V}{a}\phi^{\gamma-1} \qquad \frac{\Delta I}{\Delta\Phi}=\gamma\frac{V}{a}\phi^{\gamma-1} $$- Le rapport de transfert statique et la sensibilité sont du même ordre de grandeur (\(0,5<\gamma<1\))
- La cellule photoconductrice est un capteur non linéaire, la sensibilité décroît avec le flux, (sauf si \(\gamma=1\)). On peut toujours travailler en petits signaux.
- La sensibilité est proportionnelle à la tension appliquée, mais une augmentation de la tension augmente la puissance dissipée et élève la température du capteur ce qui dégrade ses performances.
Sensibilité et sensibilité spectrale
Compte tenu des relations précédemment établies : $$ I_p=qFG = q\frac{\tau_n \mu V}{L^2}\eta\frac{(1-r)\lambda}{hc}\Phi(\lambda)\quad(\lambda\leq\lambda_s)$$ avec \(\tau_n\) fonction de \(Phi(\lambda)\) et \(\eta\), \(r\) fonction de \(\lambda\).

Typiquement la sensibilité est de \(10^{-1} - 10^2\) A/W selon le matériau utilisé, et ce pour une tension appliquée de 10V et une surface réceptrice de 1 cm\(^2\).
Temps de réponse et Réponse en fréquence
Dans le cas d'un éclairement modulé, le temps de réponse est lié au temps d'établissement du régime d'équilibre décrit précédemment. Il est selon les matériaux de 0,1 µs à 100 ms.
En pratique, on peut considérer une cellule photoconductrice comme un système du premier ordre avec une fréquence de coupure de l'ordre de 10\(^2\)Hz à 10\(^5\)Hz.
Il faut distinguer ce temps de réponse de la résistance du temps de réponse électrique dans le cas d'un circuit où la résistance serait associée à un condensateur (eg. \(\tau=RC\)).
Détectivité
Typiquement, elle de l'ordre de 10\(^8\) à 10\(^{11}\) cm.Hz\(^{0,5}\).W\(^{-1}\), au maximum de la sensibilité spectrale.
Utilisation / Applications
Photodiode
Jonction PN
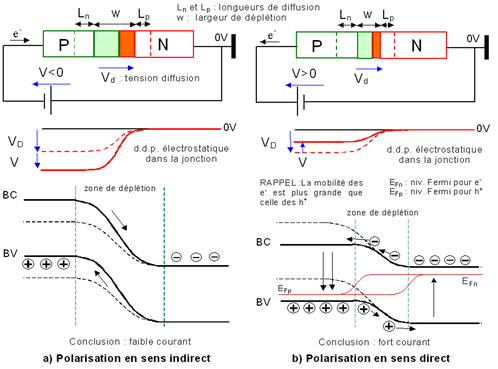
Expression du courant
$$I=I_o \exp\left(\frac{q v_d}{kT}\right) - I_o $$Pour \(\displaystyle v_d << -\frac{kT}{q} \approx -26\,\textrm{mV} \) : $$I_r = I_o$$ C'est le courant inverse de la diode.
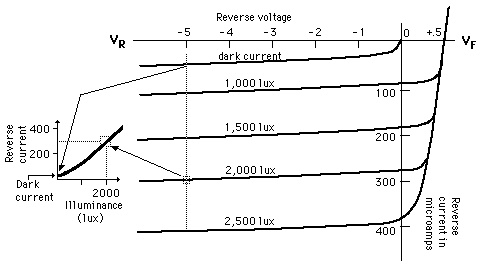
Absorption d'un photon

Le courant inverse devient : $$I_r= - I_o \exp\left(\frac{q v_d}{kT}\right) + I_o + I_p $$
avec : $$I_p=\frac{q\eta(1-r)\lambda}{hc}\Phi\exp(-\alpha w_p)$$
Pour une polarisation inverse \(v_d\) suffisante : $$I_r=I_o+I_p$$
et pour un éclairement suffisant : $$I_r=I_p$$
Circuit et droite de charge
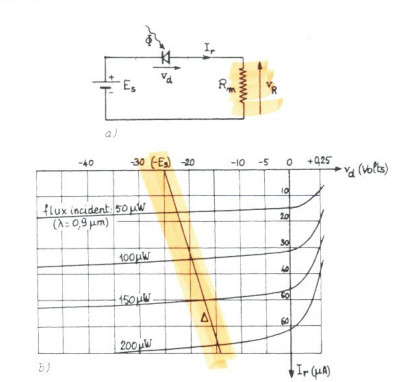
L'équation du circuit (droite charge) s'écrit: $$ E= R_mI_r - v_d$$
Elle permet de déterminer le point de fonctionnement \(Q\), autour duquel le capteur est linéaire avec une sensibilté : $$S(\lambda)=\frac{\Delta I_p}{\Delta\Phi}= \frac{q\eta(1-r)\lambda}{hc}\exp(-\alpha w_p)$$