UE transdisciplinaire - Physique
Imagerie calcique - Visualisation de l'influx nerveux
Benoît C. FORGET
2015-2016
Laboratoire neurophotonique
UFR des Scicences Fondamentales et Biomédicales
benoit.forget@parisdescartes.fr


Calcium : indicateur de l'activité
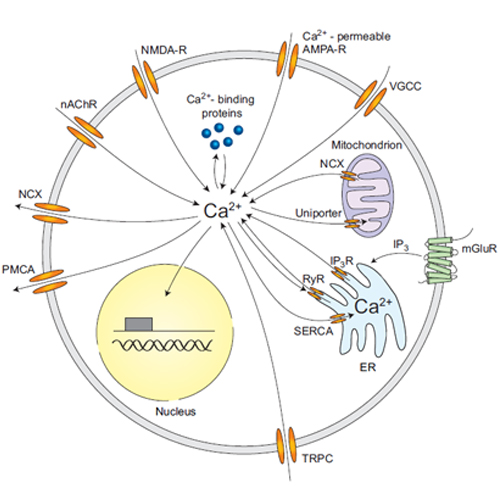
Microscopie à fluorescence


Plan
- Microscopie à fluorescence : Rappels
- Microscope : Rappels d'optique géométrique
- Fluorescence
- De l'image à la mesure quantitative : Où ? , Combien ?, Quand ?
- Où ? : Notion de résolution spatiale
- Nature ondulatoire de la lumière
- L'expérience de fentes d'Young
- Un peu (un tout petit peu) de maths : la décomposition en séries de Fourier
- La limite de résolution
- Combien ? : Compter les photons
- Un peu (un tout petit peu) de mécanique quantique
- Fluctuations aléatoires : Rapport signal sur bruit
- Statistique de Poisson
- Quand ? : résolution temporelle
Qu’est ce qu’un microscope?
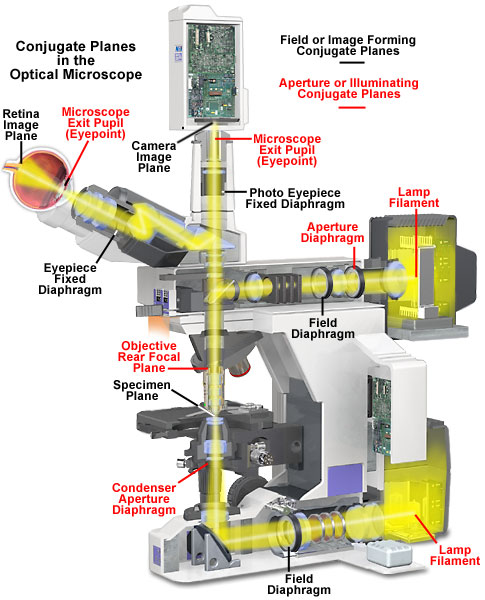
Instrument qui:
- donne une image grossie d’un petit objet (grossisement)
- sépare les détails de celui-ci sur l’image (résolution)
- rend les détails visibles à l’œil ou avec une caméra
Excellent site sur la microscopie en général : Nikon microscopy U
Qu’est ce qu’un microscope?

Instrument qui:
- donne une image grossie d’un petit objet (grossisement)
- sépare les détails de celui-ci sur l’image (résolution)
- rend les détails visibles à l’œil ou avec une caméra
Formation d'image

- le système est stigmatique pour les points \(A\) et \(A'\) ;
- \(A'\) est le point conjugué du point \(A\) : \(A'\) est l'image \(A\) ;
- tout rayon lumineux dont le support dans le milieu incident passe par \(A'\) a son support dans le milieu émergeant passant par \(A'\) ;
- en l'absence de stigmatisme, l'image est floue
image nette


On cherche une relation bijective entre l' "objet" et l' "image" : pouvoir retrouver l' "objet" à partir de l' "image"
Optique géométrique
- rayon lumineux pour étudier la propagation de la lumière et la formation d'images ;
- lois empiriques de propagation rectiligne, de réflexion et réfraction ;
- permet la conception d'instruments (eg. télescope, microscope, fibres optiques ...)

Wall painting from the Stanzino delle Matematiche in the Galleria degli Uffizi (Florence, Italy). Painted by Giulio Parigi (1571-1635) in the years 1599-1600.

Microscope Zeiss, circa 1879, d'autres de la même époque ici : Museum optischer Instrumente
Dioptres

Rélexion et Réfraction : A l'interface entre deux milieux d'indice de réfraction différents, le rayon "change de direction".
Snell - Descartes

- Réflexion : $$ i = -r $$
- Réfraction : $$ n_1 \sin i_1 = n_2 \sin i_2 $$
- Conditions de Gauss : $$ \sin i \approx i $$
- Retour inverse de la lumière
Mais que regarde Venus ?
Véronese 1585 : Vénus au miroir
lentille mince
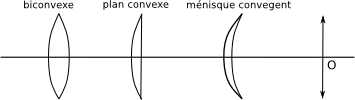

Relation de conjugaison
$$ \frac{1}{\overline{OA'}}-\frac{1}{\overline{OA}}=\frac{1}{\overline{OF'}} \left(=-\frac{1}{\overline{OF}} \right) $$Notion de foyer
Le foyer est le point conjugué de l'infini
Même les systèmes complexes ont un seul foyer objet et un seul foyer image
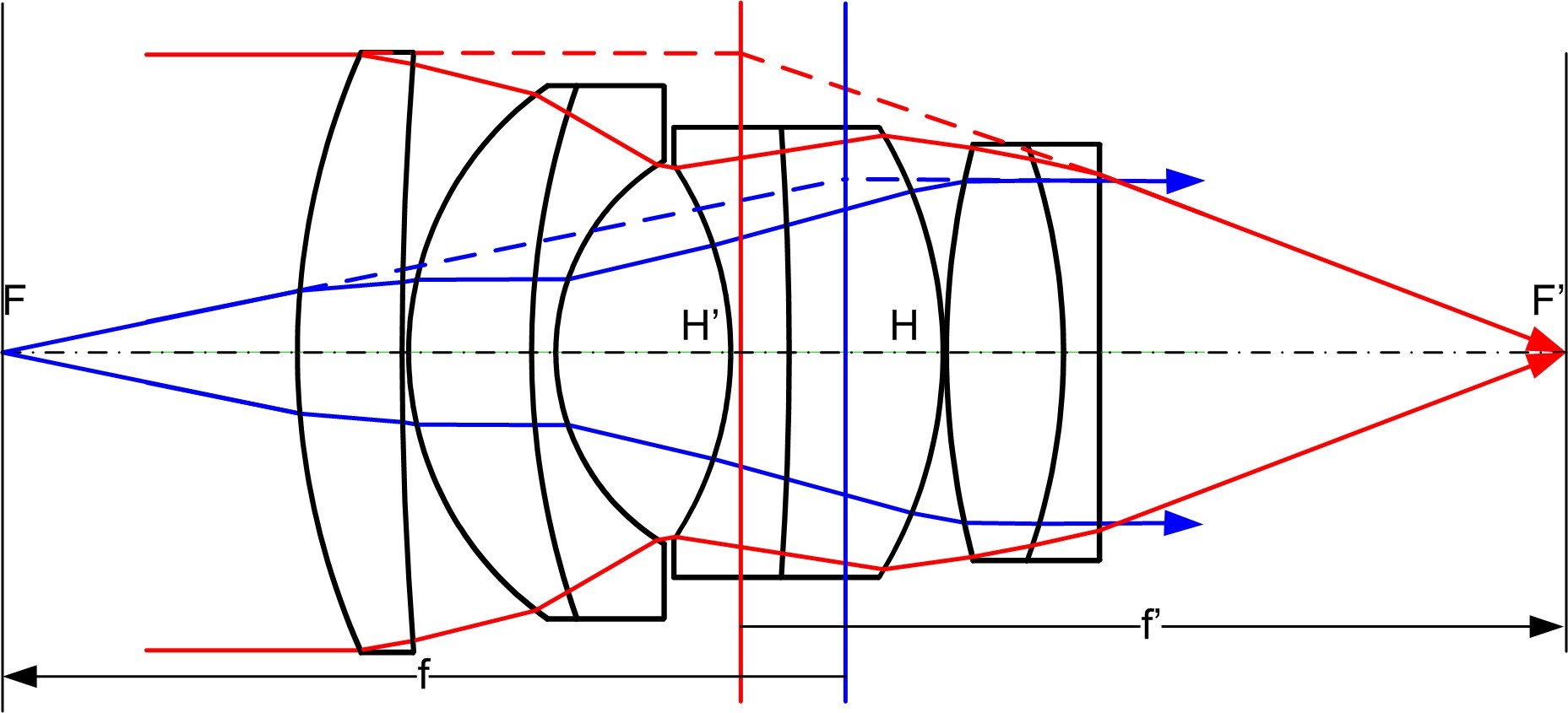
Grandissement transverse
$$ \gamma_t = \frac{\overline{A'B'}}{\overline{AB}}=\frac{\overline{OA'}}{\overline{OA}}$$montage afocal
loupe et grossissement angulaire
Microscope composé
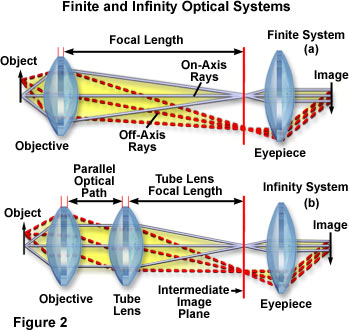
La configuration "corrigée à l'infini" est la plus couramment utilisée.
Objectif

Qu’est ce qu’un microscope?

Instrument qui:
- donne une image grossie d’un petit objet (grossisement)
- sépare les détails de celui-ci sur l’image (résolution)
- rend les détails visibles à l’œil ou avec une caméra
le grossisement ne suffit pas
Nature ondulatoire de la lumière
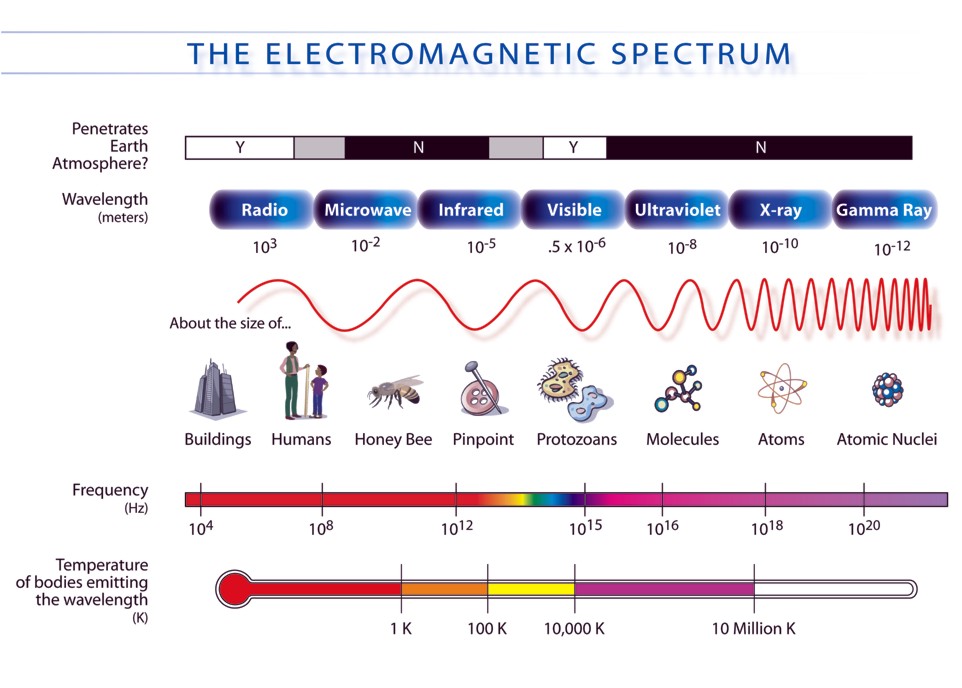
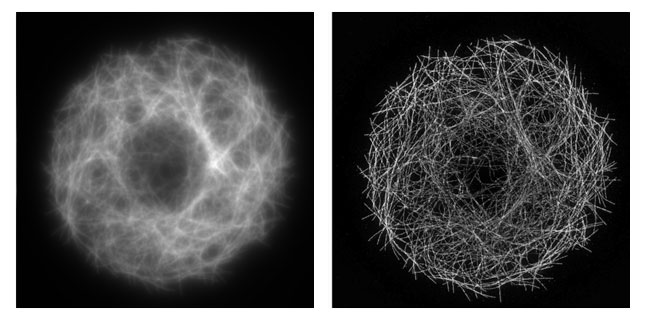
Microtubules de cellules S2 de drosophile
Suite la semaine prochaine ...
Qu’est ce qu’un microscope?

Instrument qui:
- donne une image grossie d’un petit objet (grossisement)
- sépare les détails de celui-ci sur l’image (résolution)
- rend les détails visibles à l’œil ou avec une caméra
Fluorite



Principe de la fluorescence
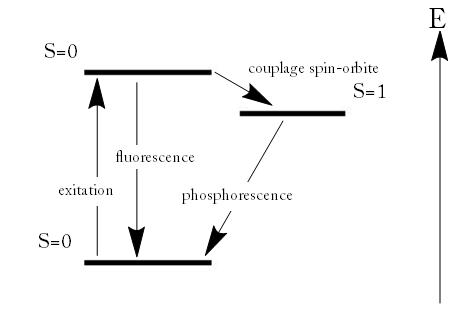
Spectres moléculaires
Cas d'une molécule diatomique stable : il existe un minimum du potentiel d’interaction entre deux atomes
Remarque : L'oscillateur harmonique
Tout système à l'équilibre peut-être (en première approximation) décrit par un potentiel parabolique :
Oscillateur harmonique
- Niveaux électroniques:
- Niveaux électroniques : niveau fondamental, niveaux excités, transitions entre niveaux (comme dans l’atome d’hydrogène).
- Transitions possibles dans le visible ou l’UV (1 à 10 eV) entre deux niveaux
- Énergie de vibration :
- Fond du puits de potentiel : approximation harmonique $$E_n = h\nu(n+1/2)\; \textrm{avec}\; \nu^2 = k/m$$
- Transitions possibles dans l’IR (0.1 eV) entre deux niveaux.
- Énergie de rotation
- Spectre de rotation \(E_r = J(J+1)\) I : moment d’inertie de la molécule
- Transitions possibles dans le domaine µ-ondes (0.001 eV) entre deux niveaux
Déplacement de Stokes
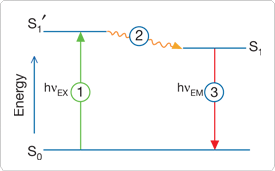

eg. Rhodamine 6g
Énergie d'un photon : $$ E = \frac{hc}{\lambda} = h\nu $$
cube
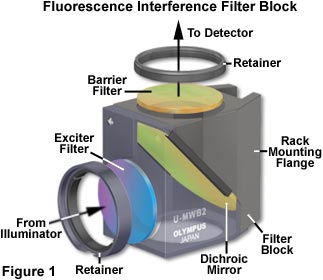
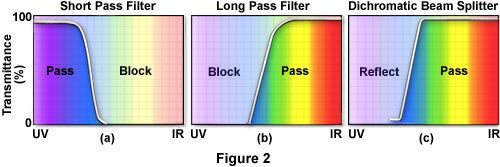

Voir des biomolécules en fluorescence
En général, les molécules biologiques (protéines, acides ne sont pas fluorescentes dans le visible (quelques exceptions: flavines, NADH, protéines fluorescentes,…). Certains acides aminés ont néanmoins des propriétés de fluorescence dans l’UV (tryptophane).
On attache spécifiquement des marqueurs fluorescents :
- couplage covalent (liaison chimique)
- marquage d’affinité: on utilise une molécule fluorescente qui vient s’attacher spécifiquement (anticorps, toxines,…)
- clonage d’une protéine fluorescente
GFP

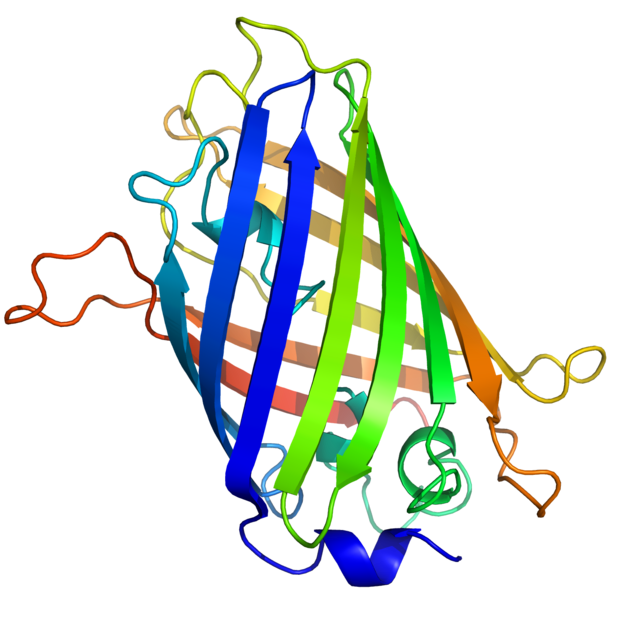
![]() : GFP
: GFP
GFP modifiée

GCaMP
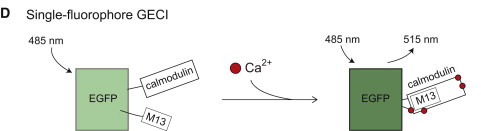
Où ?
résolution spatiale

Microtubules de cellules S2 de drosophile
Optique ondulatoire






Qu'est-ce qu'une onde ?

Dans un milieu élastique il existe des forces internes qui tendent à le ramener à sa situation d'équilibre après une perturbation
Cette perturbation (ou déformation) se déplace à une vitesse (célérité) qui est déterminée uniquement par les propriétés mécaniques de ce milieu.
A deformation moving while keeping the same shape
Space and time evolution (variables) are 'coupled':
Is there an equation that allows for solution :
$$A\xi(x-ct)+B\xi(x+ct)$$
d'Alembert equation !
$$\frac{\partial^2 \xi}{\partial t^2} - c^2 \frac{\partial^2 \xi}{\partial x^2} =0 $$
Trig functions (sine, cosine) are solution to d'Alembert's equation.
In the form :
$$\xi(x,t)= A\cos(kx \pm \omega t+ \phi ) $$
with : \(\displaystyle c=\frac{\omega}{k}\)
Space (\(\lambda\)) and time (\(T\)) periodicity are explicited :
$$\cos\left(2\pi\left(\frac{x}{\lambda} \pm \frac{t}{T}\right)+ \phi \right )$$
$$k=\frac{2\pi}{\lambda} \; ; \; \omega = 2\pi f = \frac{2\pi}{T} \quad\to \quad c=f\lambda$$
The EM field \(E(x,t)\)is written in complex notation :
\begin{align*}
E=A\cos(kx \pm \omega t + \phi) & = \Re\left\{\tilde E = Ae ^{j(kx \pm \omega t + \phi)}\right\} \\
& = \Re\left\{\tilde E = Ae ^{j\phi}e ^{j(kx \pm \omega t)}\right\} \\
& = \Re\left\{\tilde E =\tilde Ae ^{j(kx \pm \omega t)}\right\}
\end{align*}
Note: Physical (measurable) quantites can only be expressed with real numbers.
For example, a sound wave :
$$f=1000\,{\rm Hz} \; ;\; c=330\,{\rm m.s^{-1}} \quad\to\; \lambda = 0,33\,\textrm{m}$$
An image is a spatial distribution of intensity, the intensity of the total field reaching the image plane
This total field can be expressed as the sum of individual fields and the image can "viewed" as the interference pattern genrated by these individual fileds !
Any periodic function \(f(t)\) of period \(T\) (pulsation \(\omega\), \(\omega T=2\pi\)) can be expressed as :
Il en existe plusieurs :
En 1D : En 3D :
Emiliano Ronzitti
nombre de photons par unité de temps (seconde):
Solution à l'état stationnaire :
$$ \frac{dP_e}{dt} =0 \quad\to\quad k_{des}P_e =k_{exc}P_g$$
Taux de fluorescence :
$$ \Gamma = k_r P_e = \frac{1}{T_{fluo}}P_e$$
$$ \frac{S}{\sigma_b} >> 1$$
Mathematical description of waves
$$\xi(x,t) = \xi(x-ct) \qquad\left\{\xi(x+ct)\;\textrm{if}\; \vec c= -c \vec u_x \right\}$$
From a mathematical point of view

Transport d'énergie sans transport de matière

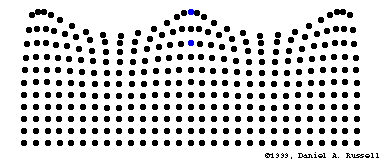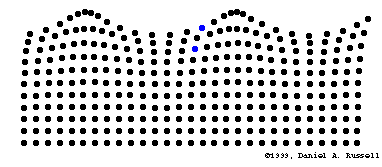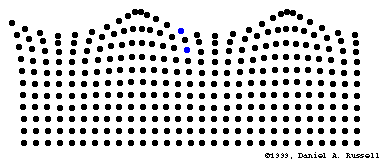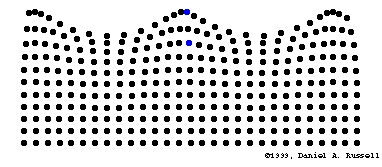
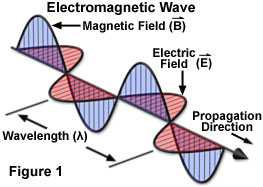
Fonctions trigonométriques
Notation complexe
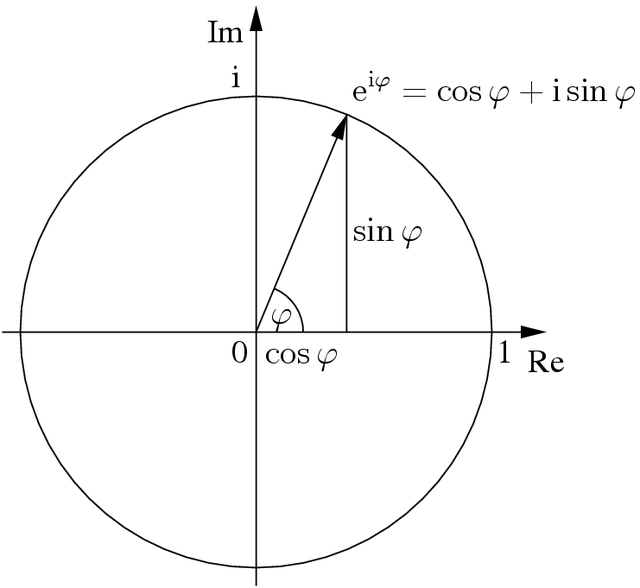
The traveling wave
$$\tilde{E}=\tilde{A}e^{j( \omega t \pm kr)}$$
Optical Waves

Visible light waves have "very high" frequency :
$$ c=3\times 10^8 {\rm m/s} \qquad 400 {\rm nm} < \lambda < 700 {\rm nm} $$
$$ f= \frac{3\times 10^8 {\rm m/s}}{500\times 10^{-9} {\rm m}} = 6\times 10^{14} {\rm Hz} $$
detector
response time
eye
\( \approx 0,1\) s
photo film
\( \approx 10^{-4} - 10^{-2} \) s
single electronic detector
\( \approx 10^{-6} - 10^{-2}\) s
CCD
\( \approx 10^{-2}\) s
Filtrage des fréquences spatiales
L'expérience de fentes d'Young
Abbe's theory of image formation
$$ d=\frac{\lambda}{2n\sin \alpha}$$
Fourier series
\begin{align*}
f(t) &= a_0 + a_1\sin\omega t + b_1 \cos\omega t + a_2\sin 2\omega t + b_2 \cos 2\omega t + \ldots \\\
&= a_0 + \sum_n a_n \sin n\omega t + \sum_n b_n \cos n\omega t
\end{align*}

Abbe's diffraction limit
PSF

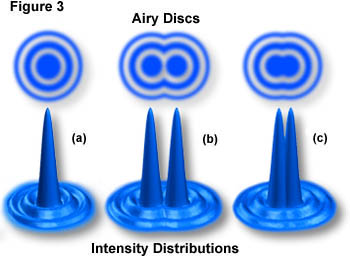
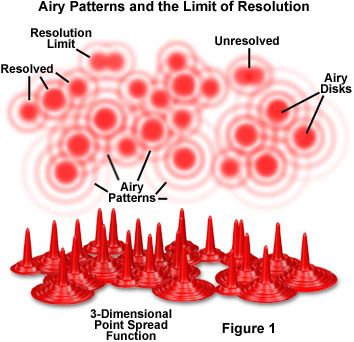

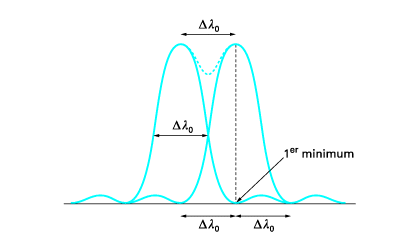
Définitions de la résolution
Tache d'Airy
 $$E(\theta) = E_0 \left ( \frac{2 J_1(ka \sin \theta)}{ka \sin \theta} \right )^2$$
$$E(\theta) = E_0 \left ( \frac{2 J_1(ka \sin \theta)}{ka \sin \theta} \right )^2$$
$$k = \frac{2\pi}{ON}$$
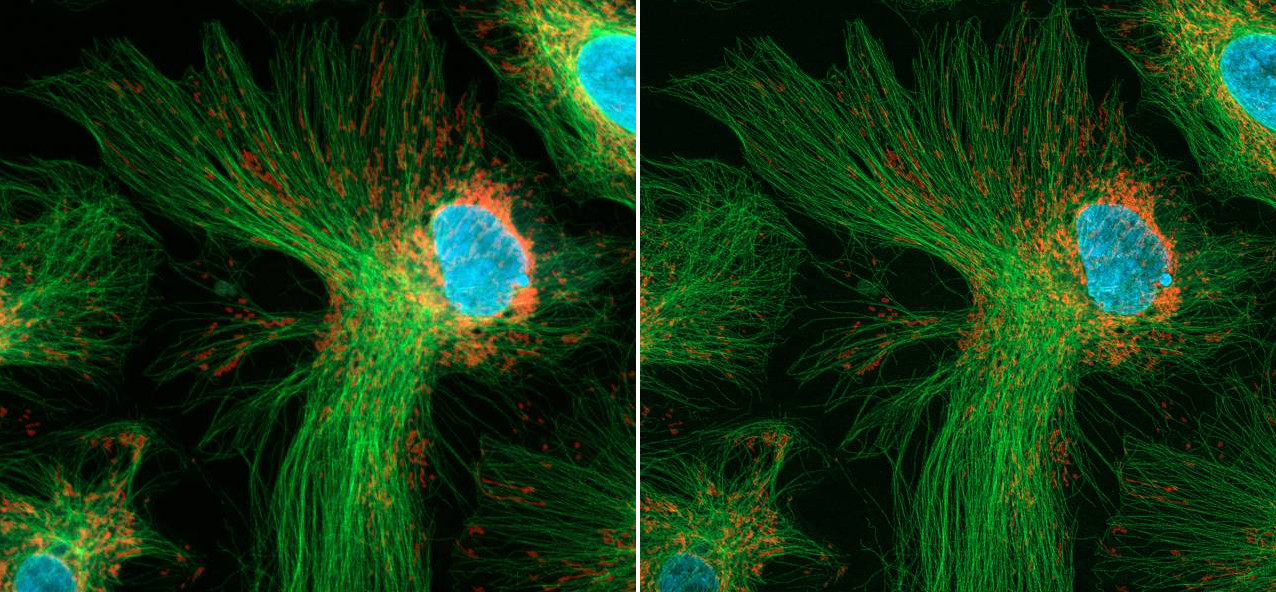
Notion de convolution ...

Convolution, filtrage, traitement d'image
... et de déconvolution


Illumination
structuréeMoiré





Modulation d'amplitude




Microscopie HiLo

Résolution axiale
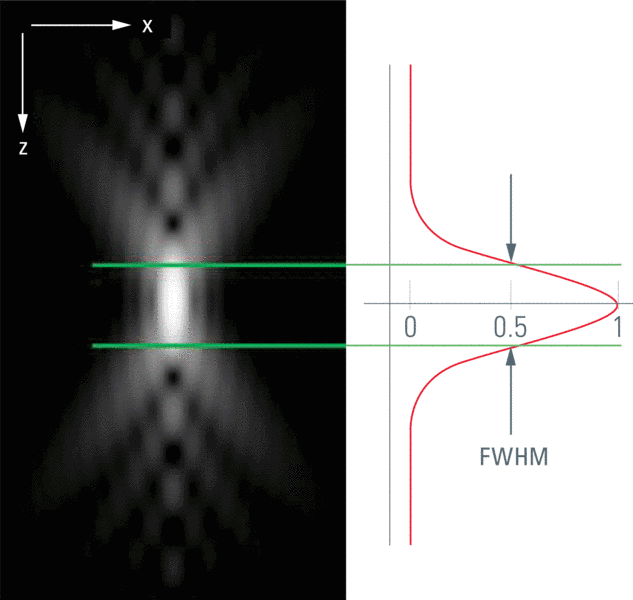
Microscopie confocale

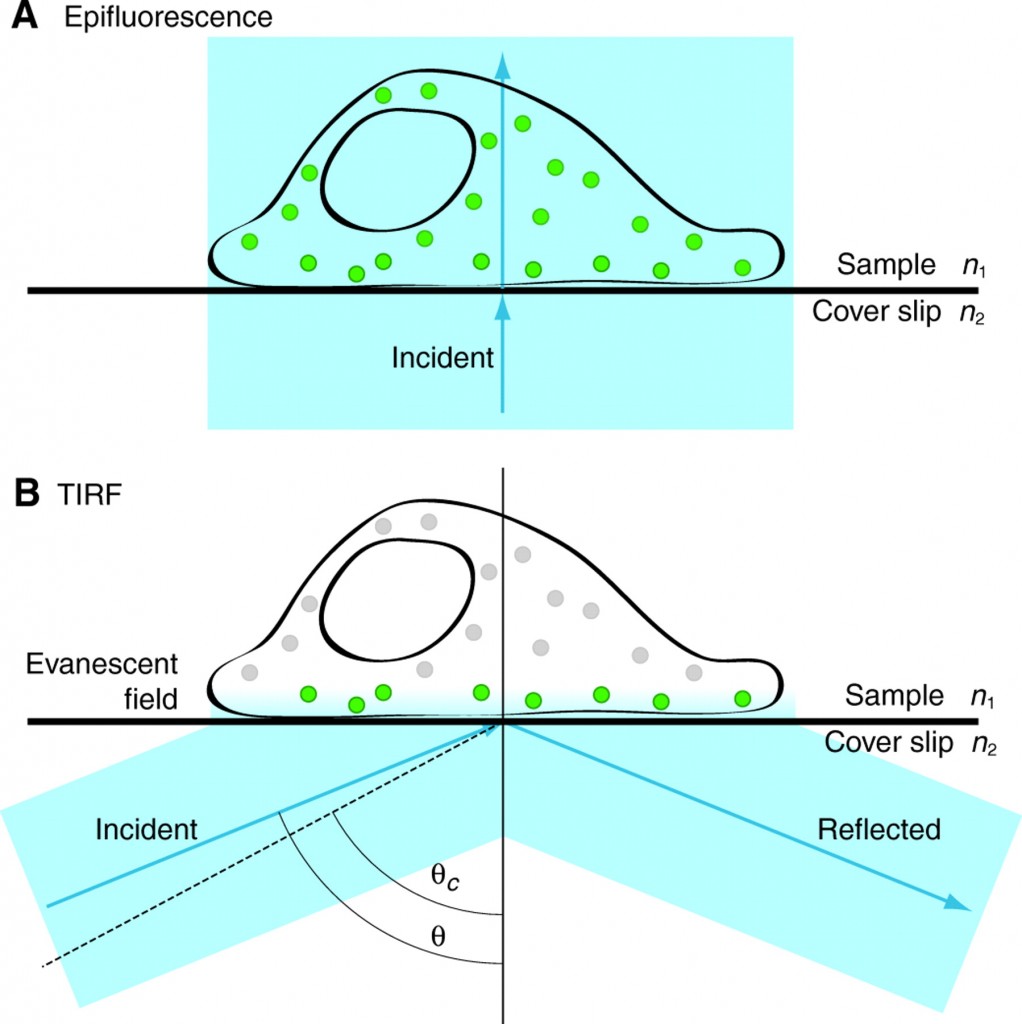
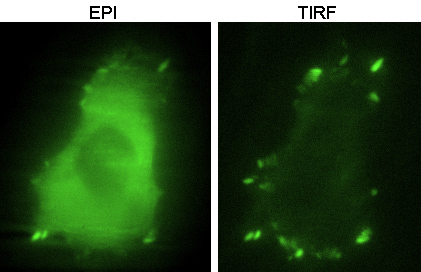
microscopie à onde évanescente : TIRF
microscopie bi-photonique

Combien ?
mesure quantitative et RSB
Nombre de photons
$$ n_i = \frac{\textrm{Énergie par unité de temps}}{\textrm{Énergie par photon}} = \frac{I}{hc/\lambda} $$
Système fluorescent à deux niveau

Dynamique des populations
\begin{align}
\frac{dP_e}{dt} &= -k_{des}P_e+k_{exc}P_g \\
P_e+P_g &=1
\end{align}
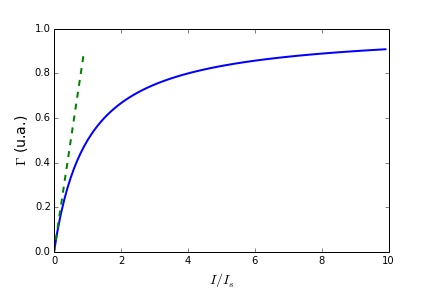
Saturation de la fluorescence
$$\Gamma=\frac{1}{T_{fluo}}\frac{I/I_s}{1+I/I_s}$$
mesure et RSB
Sources de bruit
- Bruit électronique (bruit de lecture, courant d'obscurité, ...)
indépendant de l'intensité lumineuse - Signal optique parasite (autofluorescence, lumière diffusée, ...)
proportionnel de l'intensité lumineuse - Fluctuations intrinsèque (bruit de photon ou "shot noise")
proportionnel de l'intensité lumineuse
Comme ces mécanismes sont indépendants : $$ \sigma^2=\sigma_{elec}^2+\sigma_{par}^2+\sigma_{shot}^2$$
Si on peut "minimiser" les sources de signal parasite et le bruit électronique, le bruit de photons correspond à des fluctuations dues à la nature quantique de la lumière
Une mesure "au bruit de photon" est une mesure "idéale".
Loi de Poisson
Loi de probabilité discrète décrivant le nombre d'évènements survenant pendant un laps de temps, si ces évènements :
- se produisant avec une fréquence moyenne connue
- indépendants du temps écoulé depuis l’évènement précédent
- \(\lambda\) est est un nombre positif
- Pour étudier pendant \(N\) minutes des évènement se produisant en moyenne \(n\) fois par minutes : $$ \lambda = N\times n $$
Espérance
\begin{eqnarray*} E\{X\}&=&\sum_{k=1}^{k=\infty}kP(X=k) \\ &=& \sum_{k=1}^{k=\infty}ke^{-\lambda}\frac{\lambda^k}{k!} \\ &=&e^{-\lambda}\sum_{k=1}^{k=\infty}\frac{\lambda^k}{(k-1)!} \\ &=&\lambda e^{-\lambda}\sum_{k=1}^{k=\infty}\frac{\lambda^{k-1}}{(k-1)!} = \lambda e^{-\lambda} e^{\lambda} =\lambda \end{eqnarray*}Variance
\begin{eqnarray*} V\{X\} = E\{X^2\}-(E\{X\})^2 &=& \sum_{k=1}^{k=\infty}k^2P(X=k) -\lambda^2 \\ &=& \sum_{k=1}^{k=\infty}k^2e^{-\lambda}\frac{\lambda^k}{k!} -\lambda^2 \\ &=& \lambda e^{-\lambda}\sum_{k=1}^{k=\infty}k\frac{\lambda^{(k-1)}}{(k-1)!} -\lambda^2 \\ &=& \lambda e^{-\lambda}\sum_{k=1}^{k=\infty} \frac{d}{d\lambda}\left[\frac{\lambda^k}{(k-1)!}\right] -\lambda^2 \\ \end{eqnarray*}Loi de Poisson - Loi normale
 $$ P(X=k)=e^{-\lambda}\frac{\lambda^k}{k!} \approx \frac{1}{\sqrt{2\pi\lambda}}\exp\left(-\frac{(k-\lambda)^2}{2\lambda}\right)$$
$$ P(X=k)=e^{-\lambda}\frac{\lambda^k}{k!} \approx \frac{1}{\sqrt{2\pi\lambda}}\exp\left(-\frac{(k-\lambda)^2}{2\lambda}\right)$$
Pistes futures
