Refreshers
Geometrical and Wave Optics
Benoît C. FORGET
2015-16
Laboratoire neurophotonique
Faculté des Scicences Fondamentales et Biomédicales
benoit.forget@parisdescartes.fr


Overview
- Geometrical optics
- Rays and Images
- Optical Microscope
- Wave physics
- Wave Propagation
- Mathematical Description of Waves
- Rays and Images
- Optical Microscope
- Wave Propagation
- Mathematical Description of Waves
Light propagation and Image formation

Three theoretical "frameworks" for optics
- L'optique géométrique
- "rayon lumineux" pour étudier la propagation de la lumière et la formation d'images ;
- "lois empiriques" de propagation rectiligne, de réflexion et réfraction ;
- permet la conception d'instruments (eg. télescope, microscope, fibres optiques ...)
- L'optique ondulatoire
- Modèle scalaire
- décrit les interférences, la diffraction, la diffusion, etc. ;
- applications : mesures interférométrique (très haute précision) et la spectroscopie
- Ondes électromagnétiques
- notion de polarisation
- L'optique quantique
- émission de la lumière et interaction avec les atomes, les molécules ;
- a permis en particulier le développement du laser.
geometrical (ray) optics
- Light rays propagate in a rectilinear path as they travel in a homogeneous medium
- Rays bend (and may split in two) at the interface between two dissimilar media
- Allows the design of efficient (and cool) instruments

Wall painting from the Stanzino delle Matematiche in the Galleria degli Uffizi (Florence, Italy). Painted by Giulio Parigi (1571-1635) in the years 1599-1600.

Microscope Zeiss, circa 1879, see more at Museum optischer Instrumente
Image formation and stigmatism

- le système est stigmatique pour les points \(A\) et \(A'\) ;
- \(A'\) est le point conjugué du point \(A\) : \(A'\) est l'image \(A\) ;
- tout rayon lumineux dont le support dans le milieu incident passe par \(A'\) a son support dans le milieu émergeant passant par \(A'\) ;
- en l'absence de stigmatisme, l'image est floue
image nette


Is there a bijective relation between "object" and "image" : can we recover the "object" from the "image" ?
Dioptrics
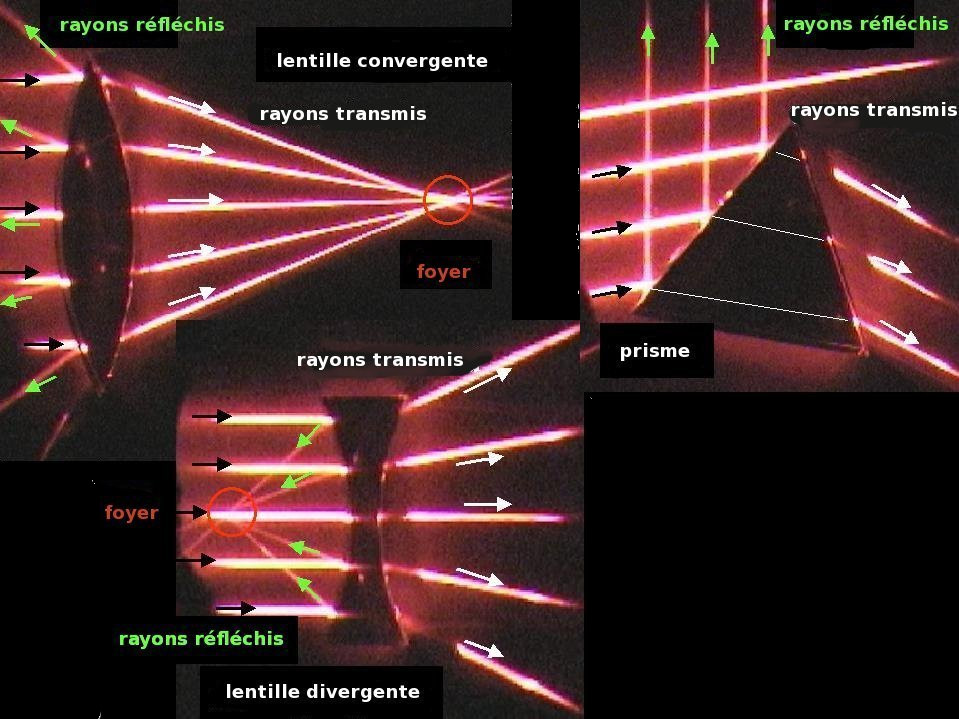
Reflection et Refraction : A at the interface between two media of different index of refraction a ray of light changes it's direction.
Snell - Descartes

- Réflexion : $$ i = -r $$
- Réfraction : $$ n_1 \sin i_1 = n_2 \sin i_2 $$
- Conditions de Gauss : $$ \sin i \approx i $$
- Retour inverse de la lumière
Who is Venus looking at ?
Véronese 1585 : Vénus au miroir
Thin lens


Descartes' conjugate equation
$$ \frac{1}{\overline{OA'}}-\frac{1}{\overline{OA}}=\frac{1}{\overline{OF'}} \left(=-\frac{1}{\overline{OF}} \right) $$focal points (planes)
The focal point is the conjugate point of infinity
More complex systems can be described with focal (and conjugate) planes

Lateral Magnification
$$ \gamma_t = \frac{\overline{A'B'}}{\overline{AB}}=\frac{\overline{OA'}}{\overline{OA}}$$Afocal system
Good online reference
Magnifying Glass, angular magnification
What is a microscope ?

Instrument qui:
- donne une image grossie d’un petit objet (grossissement)
- sépare les détails de celui-ci sur l’image (résolution)
- rend les détails visibles à l’œil ou avec une caméra
Objectif

Confocal microscopy

Magnification is not enough
What is a wave ?
What is a mechanical wave ?

In an elastic medium, internal forces tend to bring it back to its original after a perturbation
This perturbation (deformation) moves at a carateristic speed (celerity) which is solely determined by the mechanical proporties of the media
Energy transport without matter transport


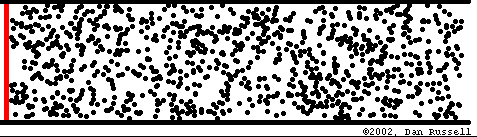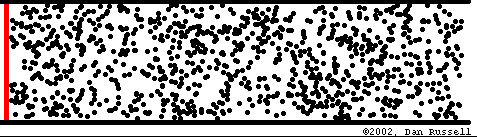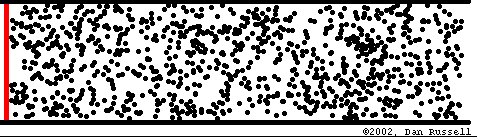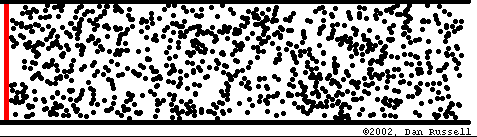

Mathematical description of waves
A deformation moving while keeping the same shape
Space and time evolution (variables) are 'coupled':
$$\xi(x,t) = \xi(x-ct) \qquad\left\{\xi(x+ct)\;\textrm{if}\; \vec c= -c \vec u_x \right\}$$
From a mathematical point of view

Is there an equation that allows for solution : $$A\xi(x-ct)+B\xi(x+ct)$$
d'Alembert equation ! $$\frac{\partial^2 \xi}{\partial t^2} - c^2 \frac{\partial^2 \xi}{\partial x^2} =0 $$
From a physical point of view
Vibrating string
Newtonian dynamics ... \(\displaystyle \to\quad \frac{\partial^2 \xi}{\partial t^2}-c^2\frac{\partial^2 \xi}{\partial x^2}=0\)
From a physical point of view
pressure wave in a sound pipe
Newtonian dynamics + fluid elasticity ... \(\displaystyle \to\quad \frac{\partial^2 p}{\partial t^2}-c^2\frac{\partial^2 p}{\partial x^2}=0\)
What about EM waves ?
 \begin{align}
\vec \nabla \cdot \vec E &= \frac{\rho}{\varepsilon_0} \\
\vec \nabla \cdot \vec B &= 0 \\
\vec \nabla \times \vec E &= -\frac{\partial\vec B}{\partial t} \\
\vec \nabla \times \vec B &= \mu_0 \vec j + \mu_0\varepsilon_0\frac{\partial\vec E}{\partial t} \\
\end{align}
\begin{align}
\vec \nabla \cdot \vec E &= \frac{\rho}{\varepsilon_0} \\
\vec \nabla \cdot \vec B &= 0 \\
\vec \nabla \times \vec E &= -\frac{\partial\vec B}{\partial t} \\
\vec \nabla \times \vec B &= \mu_0 \vec j + \mu_0\varepsilon_0\frac{\partial\vec E}{\partial t} \\
\end{align}
 $$-\nabla^2 \vec E +\mu_0\varepsilon_0 \frac{\partial^2 \vec E}{\partial t^2} = 0$$
$$ c=\frac{1}{\sqrt{\mu_0\varepsilon_0}} $$
$$-\nabla^2 \vec E +\mu_0\varepsilon_0 \frac{\partial^2 \vec E}{\partial t^2} = 0$$
$$ c=\frac{1}{\sqrt{\mu_0\varepsilon_0}} $$
trig functions as solutions
Trig functions (sine, cosine) are solution to d'Alembert's equation.
In the form : $$\xi(x,t)= A\cos(kx \pm \omega t+ \phi ) $$ with : \(\displaystyle c=\frac{\omega}{k}\)
Space (\(\lambda\)) and time (\(T\)) periodicity are explicited : $$\cos\left(2\pi\left(\frac{x}{\lambda} \pm \frac{t}{T}\right)+ \phi \right )$$ $$k=\frac{2\pi}{\lambda} \; ; \; \omega = 2\pi f = \frac{2\pi}{T} \quad\to \quad c=f\lambda$$

Optical Waves
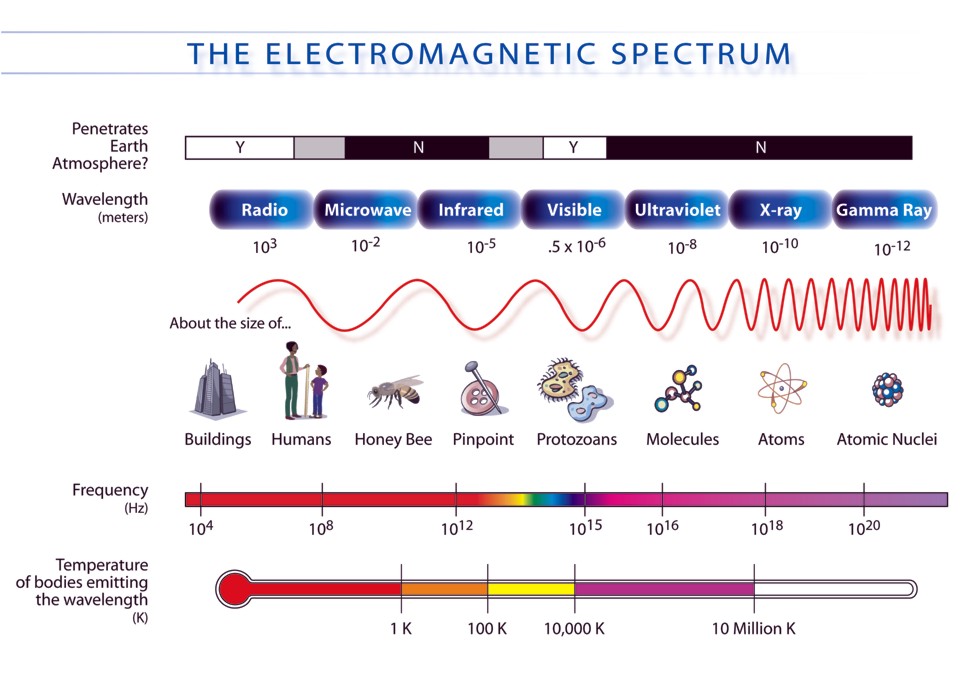
Visible light waves have "very high" frequency :
$$ c=3\times 10^8 {\rm m/s} \qquad 400 {\rm nm} < \lambda < 700 {\rm nm} $$ $$ f= \frac{3\times 10^8 {\rm m/s}}{500\times 10^{-9} {\rm m}} = 6\times 10^{14} {\rm Hz} $$| detector | response time |
| eye | \( \approx 0,1\) s |
| photo film | \( \approx 10^{-4} - 10^{-2} \) s |
| single electronic detector | \( \approx 10^{-6} - 10^{-2}\) s |
| CCD | \( \approx 10^{-2}\) s |
Complex notation

The EM field \(E(x,t)\)is written in complex notation : \begin{align*} E=A\cos(kx \pm \omega t + \phi) & = \Re\left\{\tilde E = Ae ^{j(kx \pm \omega t + \phi)}\right\} \\ & = \Re\left\{\tilde E = Ae ^{j\phi}e ^{j(kx \pm \omega t)}\right\} \\ & = \Re\left\{\tilde E =\tilde Ae ^{j(kx \pm \omega t)}\right\} \end{align*}
Note: Physical (measurable) quantites can only be expressed with real numbers.
The traveling wave
$$\tilde{E}=\tilde{A}e^{j( \omega t \pm kr)}$$For example, a sound wave : $$f=1000\,{\rm Hz} \; ;\; c=330\,{\rm m.s^{-1}} \quad\to\; \lambda = 0,33\,\textrm{m}$$
Propagating wave : the phasor
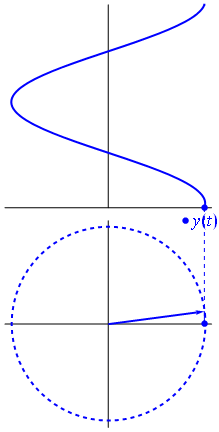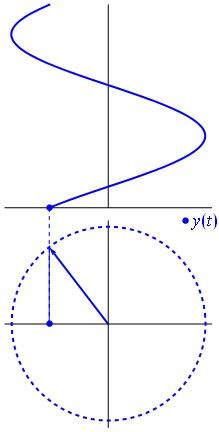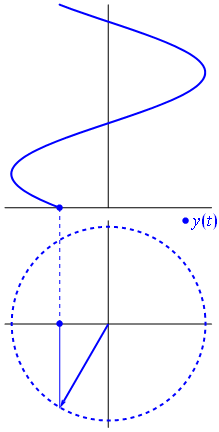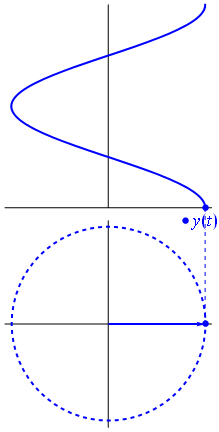
\begin{align} \omega t -kw &= \varphi_0 \\ x &= \frac{\varphi_0}{k}+\frac{\omega}{k}t \\ &= \frac{\varphi_0}{k}+ct \end{align}
One particular "point" of phase \(\varphi_0\) travels along the axis \(Ox\) at speed \(c\).
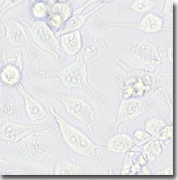
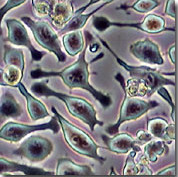
Using phase for contrast
Seeing water in water

Intensity constrast
Brightfield reflectance microscopy is based on intensity constrast
$$ R=\frac{\left(n_1-n_2\right)^2}{\left(n_1+n_2\right)^2} $$
The cell is not verry "optically different" than the sourounding medium :
Cell : \(n = 1, 36 \,\to\, R\approx 0, 0233\)
nutriment medium : \(n = 1, 335 \,\to\, R \approx 0, 0206\)
Contrast : \( \displaystyle C=\frac{I_{max}-I_{min}}{I_{max}+I_{min}} \approx 6\% \)
Why not measure phase contrast

$$\Delta\varphi = k\Delta(nz) = \frac{2\pi}{\lambda}z\Delta n$$ $$z=6 µm\,;\, \Delta n =0,025 \,;\, \lambda=0,5 µm$$ $$\Delta (nz)=\frac{\lambda}{4}\,;\,\Delta\varphi \approx \frac{\pi}{2} $$
Amplitude, phase and intensity
Remember the expression of the field (in complex and real notations) : $$ \tilde E = \tilde A e^{j(kr - \omega t)} $$ $$ \Re\{E\} = A \cos (kr - \omega t + \varphi) $$
Only the intensity (average value over tile of the energy of the wave) can be detected. $$ I = \left < E^2 \right > = \frac{1}{2} EE^* = \frac{A^2}{2} $$
Detection of the intensity is phase independant !
Interferences
D'Alembert's equation is linear
The sum of the wave (interference) is also a wave : $$ E_1 = \tilde A e^{j(kr - \omega t)} \qquad E_2 = \tilde A e^{j(kr - \omega t+\Delta \phi)} $$
The intensity of this interference is phase dependant : $$ I_T = \frac{1}{2} (E_1+E_2)(E_1+E_2)^* = I_1+I_2+2\sqrt{I_1I_2}\cos \Delta\phi $$
it is a function of the phase difference \(\Delta \varphi\) between the two intefering waves.
Improved contrast

More to come ...
- Optical Wavefront
- 2D and 3D Waves
- From Wave Optics back to Geometrical Optics
- Wavefront Engineering
- The Point Spread Function (PSF)
- Abbe's theory of image formation
- Diffraction limited focus
- PSF, Convolution and Image Resolution