Optical Wavefront


Benoît C. FORGET

2015-2016

Laboratoire neurophotonique
UFR des Scicences Fondamentales et Biomédicales
benoit.forget@parisdescartes.fr


Overview

  • 2D and 3D Waves
  • From wave optics back to ray optics
  • Wavefront Engineering

The traveling wave

$$\tilde{E}=\tilde{A}e^{j( \omega t \pm kr)}$$

For example, a sound wave : $$f=1000\,{\rm Hz} \; ;\; c=330\,{\rm m.s^{-1}} \quad\to\; \lambda = 0,33\,\textrm{m}$$

$$e^{j(\omega t - kx)}$$
$$e^{j(\omega t + kx)}$$

Propagating wave : the phasor

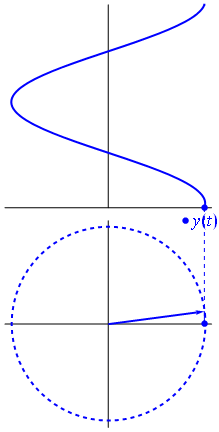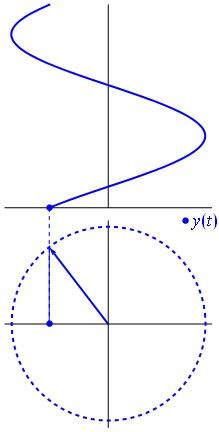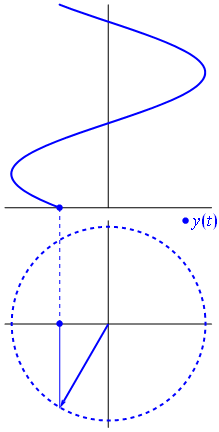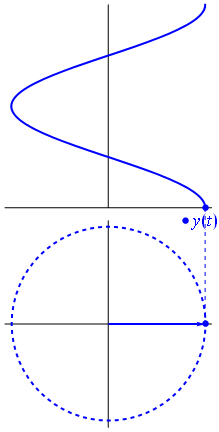
\begin{align} \xi(x+\Delta x,t) &= \tilde A e^{j(\omega t -k(x+\Delta x))} \\ &= \tilde A e^{j(\omega t -k(x))}e^{-jk\Delta x} \\ &= \xi(x,t) e^{-jk\Delta x} \end{align}
\begin{align} \omega t -kw &= \varphi_0 \\ x &= \frac{\varphi_0}{k}+\frac{\omega}{k}t \\ &= \frac{\varphi_0}{k}+ct \end{align}

One particular "point" of phase \(\varphi_0\) travels along the axis \(Ox\) at speed \(c\).

2D - 3D waves : the wavefront

In 2D (3D) a given path (surface) of same phase form a "wavefront"


The wave vector

The wave vector indicates the (local) direction of propagation of the wave.

For the "locally plane" wavefront : $$ \vec k\cdot \vec r = \rm{cst} $$

The wave vector is normal to the wave front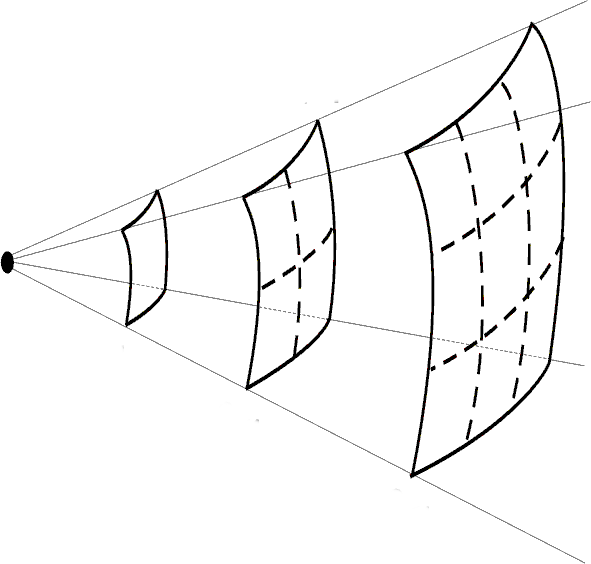

$$ \vec k\cdot \vec r = {\rm cst} \quad\to \quad \tilde{E}=\tilde{A}e^{j( \omega t \pm \vec k \cdot \vec r)}$$

from wave optics back to ray optics

Snell's law : refraction

Diffrent thickness \(\to\) different phase shift (retardation).
$$ \Delta \varphi(x) = 2\pi (n-1) \frac{x \tan \alpha}{\lambda}$$

Axicon

lens

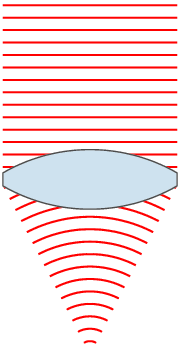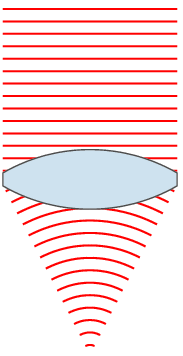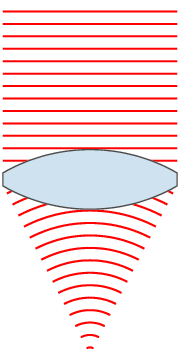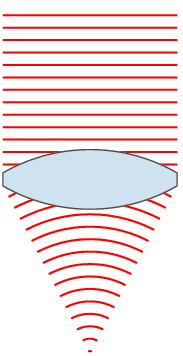
Wavefront engineering

Tilt

$$\Delta\phi_g=a\left(x\tan\theta_x+y\tan\theta_y\right)$$

Lens

$$\phi_\ell=b\Delta z\left(x^2+y^2\right)$$

Multi spots

$$\phi=\textrm{arg }\left(\sum_1^N u_n e^{i\left(\phi_g+\phi_\ell\right)}\right)$$

Wavefront Engineering

Diffractive Optical Elements (DOE)

For any point (x,y) of the incoming wavefront we want to add independantly the appropriate phase delay

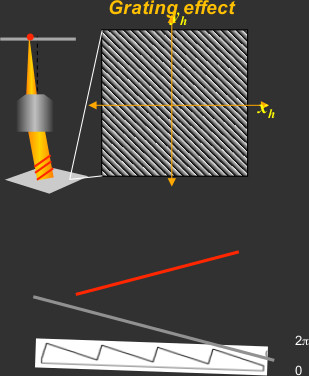$$\Delta\phi_g=a\left(x\tan\theta_x+y\tan\theta_y\right)\textrm{mod }2\pi$$
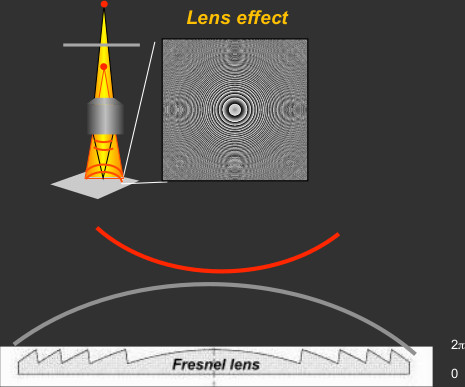$$\phi_\ell=b\Delta z\left(x^2+y^2\right)\textrm{mod }2\pi$$
$$\phi=\textrm{arg }\left(\sum_1^N u_n e^{i\left(\phi_g+\phi_\ell\right)}\right)\textrm{mod }2\pi$$

Liquid crystal spatial light modulator (SLM)

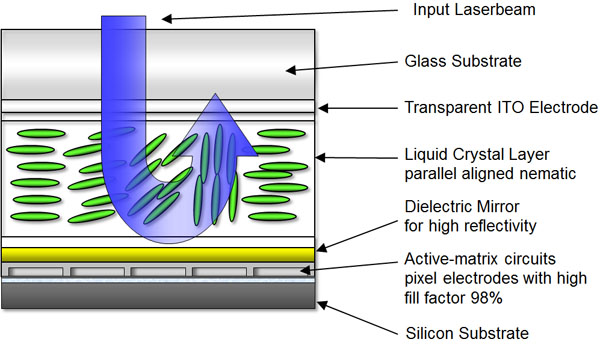
Conclusion

  • Phase modulation in back focal plane can shape intensity in the focal plane
  • Phase profiles can be calculated (to a pretty good approximation) for any shape
  • SLMs are flexible and cool tools
  • Fourier optics is your friend